
【题目】已知函数f(x)满足f(﹣x)=f(x),f(x+8)=f(x),且当x∈(0,4]时f(x)= ![]() ,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
A.(﹣ ![]() ln6,ln2]
ln6,ln2]
B.(﹣ln2,﹣ ![]() ln6)
ln6)
C.(﹣ln2,﹣ ![]() ln6]
ln6]
D.(﹣ ![]() ln6,ln2)
ln6,ln2)
【答案】C
【解析】解:∵函数f(x)满足f(﹣x)=f(x),f(x+8)=f(x),
∴函数f(x)是偶函数,且周期是8,则在[﹣2016,2016]上共有504个周期,
∵不等式在[﹣2016,2016]上有且只有2016个整数解,∴在一个周期上有且只有4个整数解,
由偶函数的性质可得,在(0,4]上有且只有2个整数解,
∵当x∈(0,4]时f(x)= ![]() ,∴则f′(x)=
,∴则f′(x)= ![]() ,
,
当f′(x)>0得1﹣ln(2x)>0,即ln(2x)<1,
即0<2x<e,即0<x< ![]() ,
,
由f′(x)<0得1﹣ln(2x)<0,得ln(2x)>1,
即2x>e,即x> ![]() ,
,
即当x= ![]() 时,函数f(x)取得极大值,同时也是最大值
时,函数f(x)取得极大值,同时也是最大值
f( ![]() )=
)= ![]() =
= ![]() ,
,
即当0<x< ![]() 时,f(x)<
时,f(x)< ![]() 有一个整数解1,
有一个整数解1,
当x> ![]() 时,0<f(x)<
时,0<f(x)< ![]() 有无数个整数解,
有无数个整数解,
①若a=0,则f2(x)+af(x)>0得f2(x)>0,此时有无数个整数解,不满足条件.
②若a>0,
则由f2(x)+af(x)>0得f(x)>0或f(x)<﹣a,
当f(x)>0时,不等式由无数个整数解,不满足条件.
③当a<0时,由f2(x)+af(x)>0得f(x)>﹣a或f(x)<0,
当f(x)<0时,没有整数解,
则要使当f(x)>﹣a有两个整数解,
∵f(1)=ln2,f(2)= ![]() =ln2,f(3)=
=ln2,f(3)= ![]() ,
,
∴当f(x)≥ln2时,函数有两个整数点1,2,当f(x)≥ ![]() 时,函数有3个整数点1,2,3
时,函数有3个整数点1,2,3
∴要使f(x)>﹣a有两个整数解,
则 ![]() ≤﹣a<ln2,即﹣ln2<a≤﹣
≤﹣a<ln2,即﹣ln2<a≤﹣ ![]() ln6,
ln6,
故选:C.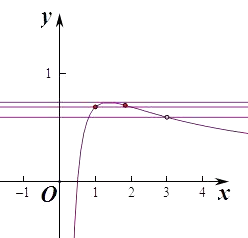


科目:高中数学 来源: 题型:
【题目】(1)问题发现
如下图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE。
填空:①∠AEB的度数为____________;
②线段AD、BE之间的数量关系是_________。

(2)拓展探究
如下图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE。请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由。
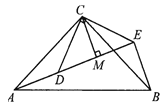
(3)解决问题
如下图,在正方形ABCD中,CD=![]() 。若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。
。若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为 . 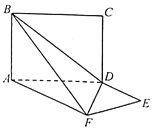
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某高中甲、乙两个班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.

(1)甲班和乙班同学身高的中位数各是多少?并计算甲班样本的方差.
(2)现从乙班这10名同学中随机抽取2名身高不低于173 cm的同学,求身高为176 cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a和b是计算机在区间(0,2)上产生的均匀随机数,则一元二次不等式ax2+4x+4b>0(a>0)的解集不是R的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 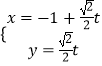 (t为参数),曲线C的极坐标方程是ρ=
(t为参数),曲线C的极坐标方程是ρ= ![]() ,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
(Ⅰ)写出直线l的极坐标方程与曲线C的普通方程;
(Ⅱ)求线段MA、MB长度之积MAMB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在坐标轴上,焦距长为2,左准线为
的中心在坐标原点,焦点在坐标轴上,焦距长为2,左准线为![]() :
: ![]() .
.
(1)求椭圆![]() 的方程及其离心率;
的方程及其离心率;
(2)若过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
(3)过椭圆![]() 右准线
右准线![]() 上任一点
上任一点![]() 引圆
引圆![]() :
: ![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .试探究直线
.试探究直线![]() 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com