
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() ,且直线
,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同轨班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)

(1)能够据此判断有97.5%把握热内加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在5—7分钟,小刚正确解得一道数学应用题所用的时间在6—8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明现正确解答完的概率;
(3)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们点答题情况进行全程研究,记A、B两人中被抽到的人数为X,求X的分布列及数学期望E(X).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 恰好经过椭圆
恰好经过椭圆![]() 的两个焦点和两个顶点.
的两个焦点和两个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)经过原点的直线![]() (不与坐标轴重合)交椭圆
(不与坐标轴重合)交椭圆![]() 于
于![]() 两点,
两点, ![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于
于![]() ,证明:以线段
,证明:以线段![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,a2﹣a1=2,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式;
(2)设bn=2log3an+1,且数列{ ![]() }的前n项和为Tn . 求Tn .
}的前n项和为Tn . 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题; 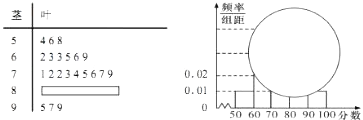
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com