
分析 由约束条件作出可行域,(x-2)2+y2的几何意义为可行域内动点(x,y)与定点P(2,0)距离的平方,然后结合点到直线的距离公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$作出可行域如图,
(x-2)2+y2的几何意义为可行域内动点(x,y)与定点P(2,0)距离的平方.
由图可知,P(2,0)与可行域内动点距离的最小值为d=$\frac{|1×2-1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
∴(x-2)2+y2的最小值等于${d}^{2}=(\frac{\sqrt{2}}{2})^{2}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
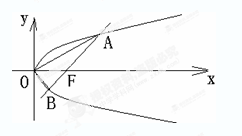 过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
过直角坐标平面xOy中的抛物线y2=2px的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )
有5位工人在某天生产同一零件,所生产零件个数的茎叶图如图所示,已知它们生产零件的平均数为10,标准差为$\sqrt{2}$,则|x-y|的值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8 | B. | 20+8$\sqrt{2}$ | C. | 16 | D. | 24+8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com