
为拉动经济增长,某市决定新建一批基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目个数分别占总数的 ,
, ,
, ,现在3名工人独立地从中任意一个项目参与建设.
,现在3名工人独立地从中任意一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率.
(2)记X为3人中选择的项目所属于基础设施工程或产业建设工程的人数,求X的分布列及数学期望.
(1) (2)2
(2)2
【解析】记第i名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件Ai,Bi,Ci,i=1,2,3.由题意,知A1,A2,A3相互独立,B1,B2,B3相互独立,C1,C2,C3相互独立,Ai,Bj,Ck(i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(Ai)= ,P(Bj)=
,P(Bj)= ,P(Ck)=
,P(Ck)= .
.
(1)他们选择的项目所属类别互不相同的概率
P= ×P(A1B2C3)=6P(A1)P(B2)P(C3)=6×
×P(A1B2C3)=6P(A1)P(B2)P(C3)=6× ×
× ×
× =
= .
.
(2)设3名工人中选择的项目属于民生工程的人数为η,
由已知η~B ,且X=3-η
,且X=3-η
所以P(X=0)=P(η=3)=
 3=
3=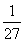 ,
,
P(X=1)=P(η=2)=
 2
2 =
= ,
,
P(X=2)=P(η=1)=

 2=
2= ,
,
P(X=3)=P(η=0)=
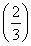 3=
3= ,
,
故X的分布列是
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X的数学期望是E(X)=0× +1×
+1× +2×
+2× +3×
+3× =2.
=2.


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用3练习卷(解析版) 题型:填空题
已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用20练习卷(解析版) 题型:填空题
设α和β为不重合的两个平面,给出下列命题:
①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
②若α外一条直线l与α内的一条直线平行,则l和α平行;
③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.
上面命题中,真命题的序号______(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用19练习卷(解析版) 题型:解答题
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用18练习卷(解析版) 题型:解答题
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).

(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用17练习卷(解析版) 题型:解答题
无锡学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设ξ为选出的人中既会唱歌又会跳舞的人数,且P(ξ>0)=
(1)求文娱队的队员人数;
(2)写出ξ的概率分布列并计算E(ξ).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,以椭圆 =1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B、C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是________.
=1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B、C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练4练习卷(解析版) 题型:填空题
已知一个正方体的所有顶点在一个球面上.若球的体积为 π,则正方体的棱长为________.
π,则正方体的棱长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com