
【题目】如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
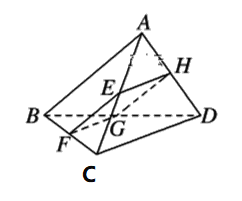
(1)求证:AB∥平面EFGH
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
【答案】(1)证明见解析; (2) (8,12).
【解析】
(1)根据几何体的结构特征,利用线面平行的判定定理,即可证得![]() 平面
平面![]() ;
;
(2)由![]() 平面
平面![]() ,设
,设![]() ,根据四边形
,根据四边形![]() 为平行四边形,求得
为平行四边形,求得![]() ,得到四边形周长的表达式,即可求解.
,得到四边形周长的表达式,即可求解.
(1)由题意,∵四边形EFGH为平行四边形,∴EF∥HG,
∵HG平面ABD,EF![]() 平面ABD,∴EF∥平面ABD,
平面ABD,∴EF∥平面ABD,
又∵EF平面ABC,平面ABD∩平面ABC=AB,∴EF∥AB,
又∵AB![]() 平面EFGH,EF平面EFGH,∴AB∥平面EFGH.
平面EFGH,EF平面EFGH,∴AB∥平面EFGH.
同理可证,![]() 平面EFGH.
平面EFGH.
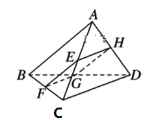
(2)设![]() ,∵四边形
,∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,则
,则![]() ,∴
,∴![]() ,
,
∴四边形EFGH的周长![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
即四边形![]() 周长的取值范围是(8,12).
周长的取值范围是(8,12).


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数y=4cos2x-4![]() sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
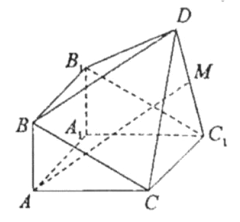
【题目】如图,由直三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求证:![]() ;
;
(II)若M为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(III)在线段BC上(含端点)是否存在点P,使直线DP与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 得值,若不存在,说明理由.
得值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com