
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为
的公差不为![]() .设
.设![]() 是数列
是数列![]()
的前![]() 项和.若
项和.若![]() 、
、![]() 、
、![]() 是数列
是数列![]() 的前
的前![]() 项,且
项,且![]() .
.
(Ⅰ)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 为等差数列,求实数
为等差数列,求实数![]() ;
;
(Ⅲ)构造数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,
,…,
若该数列前![]() 项和
项和![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() ;(Ⅲ)34.
;(Ⅲ)34.
【解析】试题分析:
(1)由题意列出方程组求得数列![]() 的首项
的首项![]() ,公差
,公差![]() ,则其通项公式为
,则其通项公式为![]() ,进一步即可求得数列
,进一步即可求得数列![]() 的通项公式为
的通项公式为![]()
(2)利用等差数列的通项公式是关于n的一次函数列出方程组,求解方程组可得![]() 或
或![]() ;
;
(3)结合题意分组求和得到关于m的方程,解方程讨论可得![]() .
.
试题解析:
(Ⅰ)设等差数列![]() 的公差为
的公差为![]() (
(![]() ),由
),由![]() 、
、![]() 、
、![]() 是数列
是数列![]() 的前
的前![]() 项,且
项,且![]()
得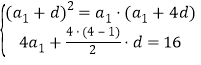 ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() 的通项公式为
的通项公式为![]() ;而
;而![]() ,
,![]() ,所以等比数列
,所以等比数列![]() 的公比
的公比![]() ,
,![]()
的通项公式为![]() ;
;
(Ⅱ)由(Ⅰ)知![]() ,因为数列
,因为数列![]() 为等差数列,所以可设
为等差数列,所以可设![]() ,
,![]() ,
,![]() ,
,
所以![]() 即
即![]() 对
对![]() 总成立,不妨设
总成立,不妨设![]() ,
,![]() ,
,![]() ,
,
则![]() 对
对![]() 总成立,取
总成立,取![]() ,
,
![]() ,
,![]() 得
得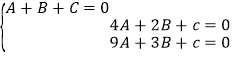 ,解得
,解得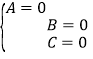 ,即
,即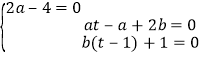 ,
,
解得![]() 或
或![]() .令
.令![]() .
.
![]() 当
当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() 为等差数列;
为等差数列;
![]() 当
当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() 为等差数列.
为等差数列.
综上,![]() 或
或![]() .
.
另解:由(Ⅰ)知![]() ,因为数列
,因为数列![]() 为等差数列,所以
为等差数列,所以![]() ,
,![]() ,
,![]() 必成等差数列,所以
必成等差数列,所以![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
令![]() .
.
![]() 当
当![]() 时,
时,![]()
![]() ,所以
,所以![]() 为等差数列;
为等差数列;
![]() 当
当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]() 为等差数列.
为等差数列.
综上,![]() 或
或![]() .
.
(Ⅲ)设从![]() 到
到![]() 各项的和为
各项的和为![]() ,则
,则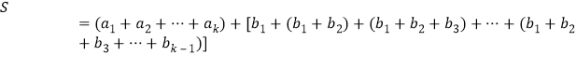
因为![]() ,所以
,所以![]()
![]()
![]() ,因此
,因此
![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,可设
,可设![]() 后面有
后面有![]() 项,则
项,则![]() ,所以
,所以![]() ,
,![]() ,因此
,因此
![]() ,即
,即![]() 的值为
的值为![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 周期为
周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①![]() 意味着每增加一个单位,
意味着每增加一个单位,![]() 平均增加8个单位
平均增加8个单位
②投掷一颗骰子实验,有掷出的点数为奇数和掷出的点数为偶数两个基本事件
③互斥事件不一定是对立事件,但对立事件一定是互斥事件
④在适宜的条件下种下一颗种子,观察它是否发芽,这个实验为古典概型
其中正确的命题有__________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m>0, ![]() ,
, ![]() .
.
(1) 若p是q的充分不必要条件,求实数m的取值范围;
(2) 若m=5,“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数x的取值范围.
”为假命题,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上的两点,则有 ![]() (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有 ![]() =(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积).
=(其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]()
![]() 1
1![]() 证明直线l经过定点并求此点的坐标;
证明直线l经过定点并求此点的坐标;
![]() 2
2![]() 若直线l不经过第四象限,求k的取值范围;
若直线l不经过第四象限,求k的取值范围;
![]() 3
3![]() 若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设![]() 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com