练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了得到函数y=sin（2x﹣ ）的图象，可以将函数y=cos2x的图象（ ）
    A.向右平移
    B.向右平移
    C.向左平移
    D.向左平移

    【答案】B
    【解析】解：由题意y=cos2x=sin（2x+ ），
    函数y=sin（2x+ ）的图象经过向右平移 ，得到函数y=sin[2（x﹣ ）+ ]= 的图象，
    故选B．
    【考点精析】通过灵活运用函数y=Asin（ωx+φ）的图象变换，掌握图象上所有点向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的倍（纵坐标不变），得到函数的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的倍（横坐标不变），得到函数的图象即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率，两焦点分别为，右顶点为， .

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设过定点的直线与双曲线的左支有两个交点，与椭圆交于两点，与圆交于两点，若的面积为， ，求正数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， 的图象在点处的切线与直线平行.

    （1）求的值；

    （2）若函数（），且在区间上是单调函数，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线： （为给定的正常数， 为参数， ）构成的集合为，给出下列命题：

    ①当时， 中直线的斜率为；

    ②中的所有直线可覆盖整个坐标平面.

    ③当时，存在某个定点，该定点到中的所有直线的距离均相等；

    ④当时， 中的两条平行直线间的距离的最小值为；

    其中正确的是__________（写出所有正确命题的编号）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）分别求函数与在区间上的极值；

    （2）求证：对任意， ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：
    ①函数y=cos（2x﹣ ）图象的一条对称轴是x=
    ②在同一坐标系中，函数y=sinx与y=lgx的交点个数为3个；
    ③将函数y=sin（2x+ ）的图象向右平移 个单位长度可得到函数y=sin2x的图象；
    ④存在实数x，使得等式sinx+cosx= 成立；
    其中正确的命题为（写出所有正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分8分） 已知抛物线C：y=-x2+4x-3 ．

    （1）求抛物线C在点A（0，－3）和点B（3，0）处的切线的交点坐标；

    （2）求抛物线C与它在点A和点B处的切线所围成的图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面为平行四边形， ， ， ， 点在底面内的射影在线段上，且， ， 为的中点， 在线段上，且．

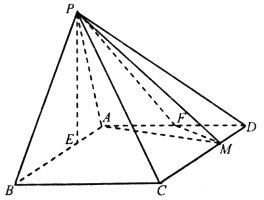
    （Ⅰ）当时，证明：平面平面；

    （Ⅱ）当平面与平面所成的二面角的正弦值为时，求四棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】咖啡馆配制两种饮料，甲种饮料分别用奶粉、咖啡、糖。乙种饮料分别用奶粉、咖啡、糖。已知每天使用原料限额为奶粉、咖啡、糖。如果甲种饮料每杯能获利元，乙种饮料每杯能获利元。每天在原料的使用限额内饮料能全部售出，每天应配制两种饮料各多少杯能获利最大?

    查看答案和解析>>

    同步练习册答案