
【题目】将![]() 名学生分成
名学生分成![]() 两组参加城市绿化活动,其中
两组参加城市绿化活动,其中![]() 组布置
组布置![]() 盆盆景,
盆盆景, ![]() 组种植
组种植![]() 棵树苗.根据历年统计,每名学生每小时能够布置
棵树苗.根据历年统计,每名学生每小时能够布置![]() 盆盆景或者种植
盆盆景或者种植![]() 棵树苗.设布置盆景的学生有
棵树苗.设布置盆景的学生有![]() 人,布置完盆景所需要的时间为
人,布置完盆景所需要的时间为![]() ,其余学生种植树苗所需要的时间为
,其余学生种植树苗所需要的时间为![]() (单位:小时,可不为整数).
(单位:小时,可不为整数).
⑴写出![]() 、
、![]() 的解析式;
的解析式;
⑵比较![]() 、
、![]() 的大小,并写出这
的大小,并写出这![]() 名学生完成总任务的时间
名学生完成总任务的时间![]() 的解析式;
的解析式;
⑶应怎样分配学生,才能使得完成总任务的时间最少?
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)见解析;(3)布置盆景和种植树苗的学生分别有
;(2)见解析;(3)布置盆景和种植树苗的学生分别有![]() 人或
人或![]() 人.
人.
【解析】试题分析:(1)设布置盆景的学生有x人,则B组人数为51-x,可求出A组所用时间![]() ,
, ![]() ,
, ![]() ,化简即可;
,化简即可;
(2)通过作差比较g(x)、h(x)的大小,确定A组与B组的所需时间,写出分段函数的解析式即可.
(3)通过两组用时比较,计算x=20与x=21时,求出总用时最少者,即可得到结果.
试题解析:
⑴由题意布置盆景的学生有![]() 人,种植树苗的学生有
人,种植树苗的学生有![]() 人,所以
人,所以![]() ,
, ![]() .
.
![]() ,
, ![]() ;
;
⑵![]() ,因为
,因为![]() 所以
所以![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]()
所以 ;
;
⑶完成总任务所用时间最少即求![]() 的最小值
的最小值
当![]() 时,
时, ![]() 递减,则
递减,则![]() .
.
故![]() 的最小值为
的最小值为![]() ,此时
,此时![]() 人
人
当![]() 时,
时, ![]() 递增,则
递增,则![]()
故![]() 的最小值为
的最小值为![]() ,此时
,此时![]() 人
人
所以布置盆景和种植树苗的学生分别有![]() 人或
人或![]() 人.
人.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
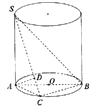
(1)求证: ![]()
(2)当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥
的离心率为e,经过第一、三象限的渐近线的斜率为k,且e≥ ![]() k.
k.
(1)求m的取值范围;
(2)设条件p:e≥ ![]() k;条件q:m2﹣(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
k;条件q:m2﹣(2a+2)m+a(a+2)≤0.若p是q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在[0,π]上的图象.
在[0,π]上的图象.

(2)若![]() 偶函数,求
偶函数,求![]()
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱A1B1C1﹣ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1 , D是棱CC1的中点.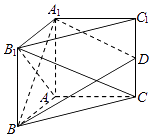
(Ⅰ)证明:平面AB1C⊥平面A1BD;
(Ⅱ)在棱A1B1上是否存在一点E,使C1E∥平面A1BD?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解1000名高一新生的身体生长状况,用系统抽样法(按等距的规则)抽取40名同学进行检查,将学生从1~1000进行编号,现已知第18组抽取的号码为443,则第一组用简单随机抽样抽取的号码为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com