
【题目】已知函数f(x)= ![]() (a>0)的导函数y=f′(x)的两个零点为0和3.
(a>0)的导函数y=f′(x)的两个零点为0和3.
(1)求函数f(x)的单调递增区间;
(2)若函数f(x)的极大值为 ![]() ,求函数f(x)在区间[0,5]上的最小值.
,求函数f(x)在区间[0,5]上的最小值.
【答案】
(1)解:f′(x)= ![]()
令g(x)=﹣ax2+(2a﹣b)x+b﹣c
函数y=f′(x)的零点即g(x)=﹣ax2+(2a﹣b)x+b﹣c的零点
即:﹣ax2+(2a﹣b)x+b﹣c=0的两根为0,3
则 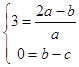 解得:b=c=﹣a,
解得:b=c=﹣a,
令f′(x)>0得0<x<3
所以函数的f(x)的单调递增区间为(0,3)
(2)解:由(1)得: ![]()
函数在区间(0,3)单调递增,在(3,+∞)单调递减,
∴ ![]() ,
,
∴a=2,
∴ ![]() ;
; ![]() ,
,
∴函数f(x)在区间[0,4]上的最小值为﹣2
【解析】(1)先求导,在根据函数的零点得到:﹣ax2+(2a﹣b)x+b﹣c=0的两根为0,3,根据韦达定理即可求出a,b,c的关系,根据导数和函数单调性的关系即可求出单调增区间,(2)根据函数的单调性即可求出函数在闭区间上的最小值.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,△ABC为等边三角形,PA=PB=PC=2,PA⊥PB,三棱锥P﹣ABC的外接球的表面积为( )
A.48π
B.12π
C.4 ![]() π
π
D.32 ![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2﹣ax,a∈R
(1)若f(x)在P(x0 , y0)(x∈[ ![]() ))处的切线方程为y=﹣2,求实数a的值;
))处的切线方程为y=﹣2,求实数a的值;
(2)若x1 , x2(x1<x2)是函数f(x)的两个零点,f′(x)是函数f(x)的导函数,证明:f′( ![]() )<0.
)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=2时,求不等式f(x)<g(x)的解集;
(2)设a> ![]() ,且当x∈[
,且当x∈[ ![]() ,a]时,f(x)≤g(x),求a的取值范围.
,a]时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2+bx+1在点(1,f(1))处的切线方程为4x﹣y﹣12=0.
(1)求函数f(x)的解析式;
(2)求f(x)的单调区间和极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设偶函数f(x)在[0,+∞)单调递增,则使得f(x)>f(2x﹣1)成立的x的取值范围是( )
A.( ![]() ,1)
,1)
B.(﹣∞, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A、B、C所对的边分别为a、b、c,且2acosB=3b﹣2bcosA. 
(1)求 ![]() 的值;
的值;
(2)设AB的中垂线交BC于D,若cos∠ADC= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com