
【题目】已知椭圆![]() ,圆
,圆![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,与圆相切与
两点,与圆相切与![]() 点,且
点,且![]() 为线段
为线段![]() 的中点,若这样的直线
的中点,若这样的直线![]() 有4条,则
有4条,则![]() 的取值范围为______.
的取值范围为______.
【答案】![]()
【解析】
分直线斜率存在和不存在两种情况各两条,![]() 根据中点弦和切线关系解出中点坐标,再根据点
根据中点弦和切线关系解出中点坐标,再根据点![]() 在椭圆内部即可解得
在椭圆内部即可解得![]() 的取值范围.
的取值范围.
根据椭圆和圆的对称性,要使这样的直线有4条,必斜率不存在的直线两条,且斜率存在的直线两条,
(i)当直线斜率不存在时,要有两条符合题意:![]()
(ii)当直线斜率存在时也有两条直线满足条件才符合题意,当![]() 时,
时,![]() 两条直线符合题意,
两条直线符合题意,
当![]() 时,先证明中点弦公式:直线
时,先证明中点弦公式:直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 为线段
为线段![]() 的中点,则
的中点,则![]()
设![]() 在椭圆上,
在椭圆上,
![]() 为线段
为线段![]() 的中点,
的中点,![]()
![]() ,
,![]() 两式相减:
两式相减:
![]()
![]()
![]()
![]()
当直线斜率存在时,设点![]() ,在圆上
,在圆上![]()
根据中点弦公式![]() ,
,
![]()
根据直线与圆相切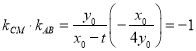
点![]() ,在圆上
,在圆上![]()
解得:![]() ,这样的点
,这样的点![]() 两个,关于x轴对称,
两个,关于x轴对称,
点![]() 在椭圆内部:
在椭圆内部:![]() 即
即![]()
解得![]() ,
,![]()
综上所述:![]()
故答案为:![]()


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数为______.
(1).设![]() 是一个区间,若对任意
是一个区间,若对任意![]() ,
,![]() ,当
,当![]() 时,都有
时,都有![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
(2).函数![]() 在定义域上是单调递减函数;
在定义域上是单调递减函数;
(3).函数![]() 在定义域上是单调递增函数;
在定义域上是单调递增函数;
(4).集合![]() 与
与![]() 相等.
相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响.经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表

摄氏温度 | —5 | 4 | 7 | 10 | 15 | 23 | 30 | 36 |
热饮杯数 | 162 | 128 | 115 | 135 | 89 | 71 | 63 | 37 |
(参考公式) ,
,
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() .样本中心点为
.样本中心点为![]() .
.
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里.因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少.统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱.请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱.请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(1)中求出的线性回归方程
.对于(1)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了纪念“一带一路”倡议提出五周年,某城市举办了一场知识竞赛,为了了解市民对“一带一路”知识的掌握情况,从回收的有效答卷中按青年组和老年组各随机抽取了40份答卷,发现成绩都在![]() 内,现将成绩按区间
内,现将成绩按区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下的频率分布直方图.
进行分组,绘制成如下的频率分布直方图.

青年组

中老年组
(1)利用直方图估计青年组的中位数和老年组的平均数;
(2)从青年组![]() ,
,![]() 的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自
的分数段中,按分层抽样的方法随机抽取5份答卷,再从中选出3份答卷对应的市民参加政府组织的座谈会,求选出的3位市民中有2位来自![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知![]() ,
, ![]() ,
,![]() ,D是边AC上的一点,将△ABC沿BD折叠,得到三棱锥A-BCD,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设BM=x,则x的取值范围是( )
,D是边AC上的一点,将△ABC沿BD折叠,得到三棱锥A-BCD,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设BM=x,则x的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王投资1万元2万元、3万元获得的收益分别是4万元、9万元、16万元为了预测投资资金x(万元)与收益y万元)之间的关系,小王选择了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根据小王选择的甲、乙两个模型,求实数a,b,c,p,q,r的值
(2)若小王投资4万元,获得收益是25.2万元,请问选择哪个模型较好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数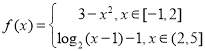 .
.
(1)在直角坐标系内直接画出![]() 的图象;
的图象;
(2)写出![]() 的单调区间,并指出单调性(不要求证明);
的单调区间,并指出单调性(不要求证明);
(3)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com