
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() 分别为
分别为![]() 的中点.
的中点.
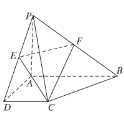
(1)求证:![]() 平面
平面![]() ;
;
(2)若截面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,求
,求![]() 的长度.
的长度.
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数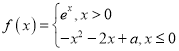 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.若![]() ,则
,则![]() 的图象上存在唯一一对关于原点
的图象上存在唯一一对关于原点![]() 对称的点
对称的点
B.存在实数![]() 使得
使得![]() 的图象上存在两对关于原点
的图象上存在两对关于原点![]() 对称的点
对称的点
C.不存在实数![]() 使得
使得![]() 的图象上存在两对关于
的图象上存在两对关于![]() 轴对称的点
轴对称的点
D.若![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则
轴对称的点,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,雨水、惊蛰、春分、清明日影之和为三丈二尺,前七个节气日影之和为七丈三尺五寸,问立夏日影长为( )
A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.
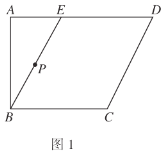
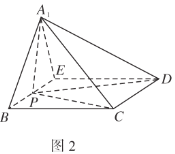
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,当直线
上,当直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,P为线段
中,P为线段![]() 上的动点,下列说法正确的是( )
上的动点,下列说法正确的是( )
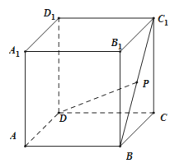
A.对任意点P,![]() 平面
平面![]()
B.三棱锥![]() 的体积为
的体积为![]()
C.线段DP长度的最小值为![]()
D.存在点P,使得DP与平面![]() 所成角的大小为
所成角的大小为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Keep是一款具有社交属性的健身APP,致力于提供健身教学、跑步、骑行、交友及健身饮食指导、装备购买等一站式运动解决方案.Keep可以让你随时随地进行锻炼,记录你每天的训练进程.不仅如此,它还可以根据不同人的体质,制定不同的健身计划.小明根据Keep记录的2019年1月至2019年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.根据该折线图,下列结论正确的是( )
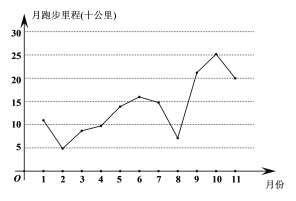
A.月跑步里程最小值出现在2月
B.月跑步里程逐月增加
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 底面
底面![]() ,
,![]() 是等边三角形,底面
是等边三角形,底面![]() 是菱形,且
是菱形,且![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为菱形
为菱形![]() 的中心,下列结论正确的有( )
的中心,下列结论正确的有( )
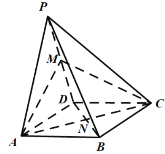
A.直线![]() 与平面
与平面![]() 平行B.直线
平行B.直线![]() 与直线
与直线![]() 垂直
垂直
C.线段![]() 与线段
与线段![]() 长度相等D.
长度相等D.![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com