
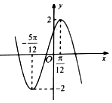
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
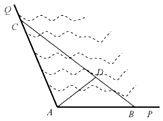 如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.
如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
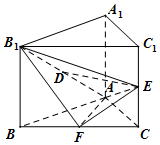 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com