
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点
的右顶点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)由双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点可得
)的顶点可得![]() 再由椭圆
再由椭圆![]() 经过点
经过点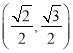 可得
可得 ![]() ,从而可得求椭圆
,从而可得求椭圆![]() 的方程;(2)设直线
的方程;(2)设直线![]() :
: ![]() ,联立
,联立![]() :
: ![]() ,得
,得![]() ,根据韦达定理及三角形面积公式将当
,根据韦达定理及三角形面积公式将当![]() 的面积用
的面积用![]() 表示,利用基本不等式等号成立的条件,可得当
表示,利用基本不等式等号成立的条件,可得当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
试题解析:(1)由已知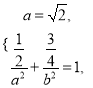 得
得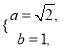
所以![]() 的方程为
的方程为![]() .
.
(2)由已知结合(1)得, ![]() ,
, ![]() ,
,
所以设直线![]() :
: ![]() ,联立
,联立![]() :
: ![]() ,得
,得![]() ,
,
得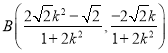 ,
,
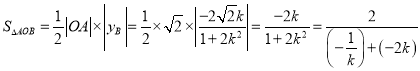 (
(![]() ),
),
当且仅当![]() ,即
,即![]() 时,
时, ![]() 的面积取得最大值,
的面积取得最大值,
所以![]() ,此时
,此时![]() ,
,
所以直线![]() :
: ![]() ,联立
,联立![]() ,解得
,解得![]() ,
,
所以![]() ,点
,点![]() 到直线
到直线![]() :
: ![]() 的距离为
的距离为![]() ,
,
所以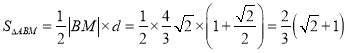 .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最值的.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mlnx﹣x2+2(m∈R).
(1)当m=1时,求f(x)的单调区间;
(2)若f(x)在x=1时取得极大值,求证:f(x)﹣f′(x)≤4x﹣3;
(3)若m≤8,当x≥1时,恒有f(x)﹣f′(x)≤4x﹣3恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是函数f(x)=msinωx﹣cosωx(m>0)的一条对称轴,且f(x)的最小正周期为π
是函数f(x)=msinωx﹣cosωx(m>0)的一条对称轴,且f(x)的最小正周期为π
(Ⅰ)求m值和f(x)的单调递增区间;
(Ⅱ)设角A,B,C为△ABC的三个内角,对应边分别为a,b,c,若f(B)=2, ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,  (t为参数).
(t为参数).
(Ⅰ)求曲线C1上的点到曲线C2距离的最小值;
(Ⅱ)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的 ![]() 倍,得到曲线
倍,得到曲线 ![]() .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 ![]() 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:

现对某城市30天的空气质量进行监测,获得30个API数据(每个数据均不同),统计绘得频率分布直方图如图.
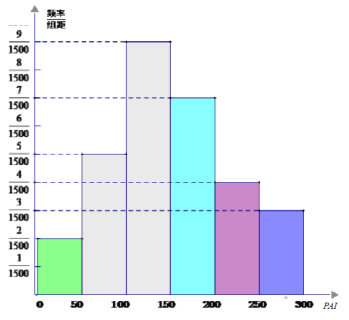
(1)请由频率分布直方图来估计这30天API 的平均值;
(2)若从获得的“空气质量优”和“空气质量中重度污染” 的数据中随机选取![]() 个数据进行复查,求“空气质量优”和“空气质量中重度污染”数据恰均被选中的概率;
个数据进行复查,求“空气质量优”和“空气质量中重度污染”数据恰均被选中的概率;
(3)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API (记为![]() )的关系式为
)的关系式为 ,
,
若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不超过600元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com