
分析 求出函数的导数,利用导函数值大于0,转化为a的表达式,求出最值即可得到a的范围.
解答 解:函数f(x)=-$\frac{1}{3}$x3+$\frac{1}{2}$x2+2ax,
f′(x)=-x2+x+2a=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$+2a.
当x∈[$\frac{2}{3}$,+∞)时,f′(x)的最大值为f′($\frac{2}{3}$)=2a+$\frac{2}{9}$,令2a+$\frac{2}{9}$>0,解得a$>-\frac{1}{9}$,
所以a的取值范围是$(-\frac{1}{9},+∞)$.
故答案为:$(-\frac{1}{9},+∞)$.
点评 本题考查函数的导数的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{15}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
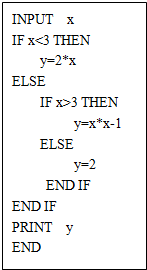
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
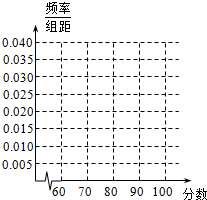 为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:
为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:| 序号 | 分组 | 频数 | 频率 |
| 1 | [60,70) | ① | 0.15 |
| 2 | [70,80) | 20 | 0.2 |
| 3 | [80,90) | 35 | 0.35 |
| 4 | [90,100) | 30 | ② |
| 合计 | 100 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,1} | C. | ∅ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{11}{5}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com