
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | B. | 若$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 | D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$是单位向量,则$\overrightarrow{a}$•$\overrightarrow{b}$=1 |
分析 根据数量积的消去律不成立,判断A错误;
根据平面向量的共线定理,列方程求出k的值,判断B错误;
根据模长公式求出$\overrightarrow{a}$•$\overrightarrow{b}$=0,判断C正确;
根据单位向量以及平面向量的数量积判断D错误.
解答 解:对于A,当$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$时,$\overrightarrow{b}$=$\overrightarrow{c}$不一定成立,A错误;
对于B,$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),当$\overrightarrow{a}$∥$\overrightarrow{b}$时,
则1×6-(-2)•k=0,解得k=-$\frac{1}{3}$,B错误;
对于C,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,得${(\overrightarrow{a}+\overrightarrow{b})}^{2}$=${(\overrightarrow{a}-\overrightarrow{b})}^{2}$,
即${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$,∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,C正确;
对于D,$\overrightarrow{a}$与$\overrightarrow{b}$是单位向量,则
$\overrightarrow{a}$•$\overrightarrow{b}$=1×1×cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=cos<$\overrightarrow{a}$,$\overrightarrow{b}$>≤1,D错误.
故选:C.
点评 本题考查了平面向量的数量积与共线定理,模长公式的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
| 月份 | 1月份 | 2月份 | 3月份 | 4月份 |
| 收购价格(元/斤) | 6 | 7 | 6 | 5 |
| 养殖成本(元/斤) | 3 | 4 | 4.6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
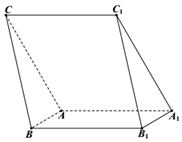 如图,三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=1.
如图,三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
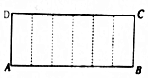 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )| A. | 13π | B. | 12π | C. | 11π | D. | 10π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
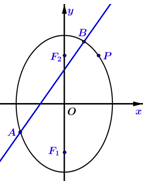 设椭圆$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)经过点$P(1,\sqrt{2})$,其离心率与双曲线x2-y2=1的离心率互为倒数.
设椭圆$M:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)经过点$P(1,\sqrt{2})$,其离心率与双曲线x2-y2=1的离心率互为倒数.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com