练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为(　　)

    A．76 B．80
    C．86 D．92

    B

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    演绎推理“因为对数函数是增函数，而函数是对数函数，所以是增函数”所得结论错误的原因是（     ）

    A．大前提错误B．小前提错误
    C．推理形式错误D．大前提和小前提都错误

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    观察下列各式：a＋b＝1，a2＋b2＝3，a3＋b3＝4，a4＋b4＝7，a5＋b5＝11，…，则a8＋b8＝(　　)

    A．28 B．47 C．76 D．123

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用反证法证明命题“若实系数一元二次方程有有理根，那么中至少有一个是偶数”时，下列假设正确的是(  )

    A．假设都是偶数B．假设都不是偶数
    C．假设至多有一个是偶数D．假设至少有两个是偶数

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示，有三根针和套在一根针上的个金属片，按下列规则，把金属片从一根针上全部移到另一根针上。

    （1）每次只能移动一个金属片；
    （2）在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面。
    若将个金属片从1号针移到3号针最少需要移动的次数记为，则=（   ）

    A．33 B．31 C．17 D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设S(n)＝，则(  )．

    A．S(n)共有n项，当n＝2时，S(2)＝
    B．S(n)共有n＋1项，当n＝2时，S(2)＝
    C．S(n)共有n2－n项，当n＝2时，S(2)＝
    D．S(n)共有n2－n＋1项，当n＝2时，S(2)＝

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为(n≥2),每个数是它下一行左右相邻两数的和,如=+,=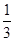+,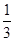=+,则第10行第4个数(从左往右数)为(　　)

    A． B．
    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某个命题与正整数n有关,若n=k(k∈N*)时命题成立,那么可推得当n=k+1时该命题也成立,现已知n=5时,该命题不成立,那么可以推得

    A．n=6时该命题不成立B．n=6时该命题成立
    C．n=4时该命题不成立D．n=4时该命题成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在证明命题“对于任意角θ,cos4θ-sin4θ=cos2θ”的过程:“cos4θ-sin4θ=(cos2θ+sin2θ)·(cos2θ-sin2θ)=cos2θ-sin2θ=cos2θ”中应用了(　　)

    A．分析法
    B．综合法
    C．分析法和综合法综合使用
    D．间接证法

    查看答案和解析>>

    同步练习册答案