Question

过三棱柱任意两个顶点的直线中，异面直线有（ ）对．

1. A.
   18
2. B.
   24
3. C.
   30
4. D.
   36

Answer 1

D
分析：直接解答，通过上下底面之间，上下底面的直线与侧面对角线与棱，侧面面对角线与棱之间三种情况分别求出异面直线的对数．
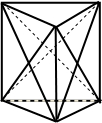
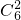
解答：解：过三棱柱任意两个顶点的直线中，所以直线共有=15条；
①三棱柱的底边三角形的边与侧面对角线、侧棱之间的异面直线，有6×3=18对，
②侧面中，一条棱对应的2条异面直线，3条棱一共就是6对．
侧面中面对角线之间6对，侧面之间的异面直线有12对．
③上下底面之间的异面直线共有6对；
满足题意的异面直线共有：18+12+6=36对．
故选D．
点评：本题考查棱柱的结构特征，异面直线的判断，排列组合的实际应用，是中档题．