
【题目】已知a∈R,函数f(x)=x3﹣3x2+3ax﹣3a+3.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈[0,2]时,求|f(x)|的最大值.
【答案】
(1)解:因为f(x)=x3﹣3x2+3ax﹣3a+3,所以f′(x)=3x2﹣6x+3a,
故f′(1)=3a﹣3,又f(1)=1,所以所求的切线方程为y=(3a﹣3)x﹣3a+4;
(2)解:由于f′(x)=3(x﹣1)2+3(a﹣1),0≤x≤2.
故当a≤0时,有f′(x)≤0,此时f(x)在[0,2]上单调递减,故
|f(x)|max=max{|f(0)|,|f(2)|}=3﹣3a.
当a≥1时,有f′(x)≥0,此时f(x)在[0,2]上单调递增,故
|f(x)|max=max{|f(0)|,|f(2)|}=3a﹣1.
当0<a<1时,由3(x﹣1)2+3(a﹣1)=0,得 ![]() ,
, ![]() .
.
所以,当x∈(0,x1)时,f′(x)>0,函数f(x)单调递增;
当x∈(x1,x2)时,f′(x)<0,函数f(x)单调递减;
当x∈(x2,2)时,f′(x)>0,函数f(x)单调递增.
所以函数f(x)的极大值 ![]() ,极小值
,极小值 ![]() .
.
故f(x1)+f(x2)=2>0, ![]() .
.
从而f(x1)>|f(x2)|.
所以|f(x)|max=max{f(0),|f(2)|,f(x1)}.
当0<a< ![]() 时,f(0)>|f(2)|.
时,f(0)>|f(2)|.
又 ![]() =
= ![]()
故 ![]() .
.
当 ![]() 时,|f(2)|=f(2),且f(2)≥f(0).
时,|f(2)|=f(2),且f(2)≥f(0).
又 ![]() =
= ![]() .
.
所以当 ![]() 时,f(x1)>|f(2)|.
时,f(x1)>|f(2)|.
故 ![]() .
.
当 ![]() 时,f(x1)≤|f(2)|.
时,f(x1)≤|f(2)|.
故f(x)max=|f(2)|=3a﹣1.
综上所述|f(x)|max= 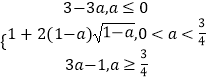 .
.
【解析】(1)求出原函数的导函数,求出函数取x=1时的导数值及f(1),由直线方程的点斜式写出切线方程;(2)求出原函数的导函数,分a≤0,0<a<1,a≥1三种情况求|f(x)|的最大值.特别当0<a<1时,仍需要利用导数求函数在区间(0,2)上的极值,然后在根据a的范围分析区间端点值与极值绝对值的大小.
【考点精析】关于本题考查的函数的最大(小)值与导数,需要了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,求
轴正半轴为极轴建立极坐标系,求![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() 两点,
两点, ![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点![]() 且互相垂直的两条直线分别与圆
且互相垂直的两条直线分别与圆![]() 交于点A,B,与圆
交于点A,B,与圆![]() 交于点C,D.
交于点C,D.

(1) 若AB=![]() ,求CD的长;
,求CD的长;
(2)若直线![]() 斜率为2,求
斜率为2,求![]() 的面积;
的面积;
(3) 若CD的中点为E,求△ABE面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为![]() 的水轮如图所示,水轮圆心
的水轮如图所示,水轮圆心![]() 距离水面
距离水面![]() ;已知水轮按逆时针做匀速转动,每
;已知水轮按逆时针做匀速转动,每![]() 转一圈,如果当水轮上点
转一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计算时间.
)开始计算时间.
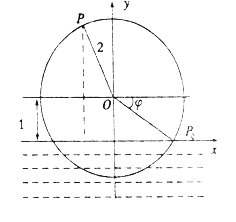
(1)以水轮所在平面与水面的交线为![]() 轴,以过点
轴,以过点![]() 且与水面垂直的直线为
且与水面垂直的直线为![]() 轴,建立如图所示的直角坐标系,将点
轴,建立如图所示的直角坐标系,将点![]() 距离水面的高度
距离水面的高度![]() 表示为时间
表示为时间![]() 的函数;
的函数;
(2)点![]() 第一次到达最高点大约要多长时间?
第一次到达最高点大约要多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的16%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金y(单位:万元),销售利润x(单位:万元)
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老张获得5.6万元的奖金,那么他的销售利润是多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为1的正六边形ABCDEF中,记以A为起点,其余顶点为终点的向量分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ;以D为起点,其余顶点为终点的向量分别为
;以D为起点,其余顶点为终点的向量分别为 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() .若m、M分别为(
.若m、M分别为( ![]() +
+ ![]() +
+ ![]() )(
)( ![]() +
+ ![]() +
+ ![]() )的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
)的最小值、最大值,其中{i,j,k}{1,2,3,4,5},{r,s,t}{1,2,3,4,5},则m、M满足( )
A.m=0,M>0
B.m<0,M>0
C.m<0,M=0
D.m<0,M<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com