
分析 (Ⅰ)当m=1时,f(x)=|x+1|-|x-2|,根据绝对值不等式的几何意义即可求出值域,
(Ⅱ)当m=-1时,不等式f(x)>3x即|x+1|+|x-2|>3x,分类讨论即可求出不等式的解集.
解答 解:(Ⅰ)当m=1时,f(x)=|x+1|-|x-2|,
∵||x+1|-|x-2||≤|(x+1)-(x-2)|=3,
∴-3≤|x+1|-|x-2|≤3,函数f(x)的值域为[-3,3],
(Ⅱ)当m=-1时,不等式f(x)>3x即|x+1|+|x-2|>3x,
①当x<-1时,得-x-1-x+2>3x,解得$x<\frac{1}{5}$,∴x<-1;
②当-1≤x<2时,得x+1-x+2>3x,解得x<1,∴-1≤x<1;
③当x≥2时,得x+1+x-2>3x,解得x<-1,所以无解;
综上所述,原不等式的解集为(-∞,1).
点评 本题考查了绝对值函数的以及绝对值不等式的解法,属于中档题.


科目:高中数学 来源: 题型:解答题
 | 1014年(1-12月) | 1015年(1-12月) | 1016年(1-11月) |
| 接单量(单) | 14463272 | 40125125 | 50331996 |
| 油费(元) | 214301962 | 591305364 | 653214963 |
| 平均每单油费t(元) | 14.82 | 14.49 | |
| 平均每单里程k(公里) | 15 | 15 | |
| 每公里油耗a(元) | 0.7 | 0.7 | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{3}$-1,$\sqrt{3}$+1] | B. | [1,3] | C. | [$\sqrt{3}$-1,2] | D. | [1,$\sqrt{3}$+1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}-1$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\sqrt{3}+1$或$\frac{{\sqrt{3}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
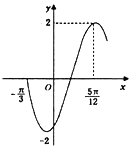 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com