
| ||
|
| 2 |
| 3 |
| ||
|
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 15 |
| 22 |
| 45 |
| 1 |
| 45 |
| 2 |
| 9 |
| 4 |
| 15 |
| 22 |
| 45 |
| 2 |
| 9 |
| 1 |
| 45 |


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
在“自选模块”考试中,某试场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(Ⅰ)求选出的4 人均为选《矩阵变换和坐标系与参数方程》的概率;
(Ⅱ)设![]() 为选出的4个人中选《数学史与不等式选讲》的人数,求
为选出的4个人中选《数学史与不等式选讲》的人数,求![]() 的分布列和
的分布列和
数学期望.
查看答案和解析>>
科目:高中数学 来源:2011届甘肃省兰州一中高三第三次模拟考试理科数学 题型:解答题
.(本小题满分12分)
在“自选模块”考试中,某考场的每位同学都选作了一道数学题,第一小组选《不等式选讲》的有1人,选《坐标系与参数方程 》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4 人均为选《坐标系与参数方程》的概率;
(2)设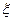 为选出的4个人中选《不等式选讲》的人数,求
为选出的4个人中选《不等式选讲》的人数,求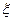 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年甘肃省高三第三次模拟考试理科数学 题型:解答题
.(本小题满分12分)
在“自选模块”考试中,某考场的每位同学都选作了一道数学题,第一小组选《不等式选讲》的有1人,选《坐标系与参数方程 》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4 人均为选《坐标系与参数方程》的概率;
(2)设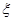 为选出的4个人中选《不等式选讲》的人数,求
为选出的4个人中选《不等式选讲》的人数,求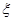 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com