
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为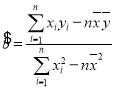 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【答案】(Ⅰ)回归直线方程为![]() ,要使月销售量不低于12万件,销售单价的最大值为8.75元;(Ⅱ)
,要使月销售量不低于12万件,销售单价的最大值为8.75元;(Ⅱ)![]() .
.
【解析】
(Ⅰ)分别求得![]() 的均值
的均值![]() ,然后计算出系数
,然后计算出系数![]() ,得回归直线方程,由回归方程可得预测值;
,得回归直线方程,由回归方程可得预测值;
(Ⅱ)把销售单价编号,写出任取2个的所有基本事件,得出指定事件所含有的基本事件的个数,由古典概型概率公式可计算出概率.
(Ⅰ)∵![]() ,
,![]() ,
,
∴![]() ,则
,则![]() ,
,
∴回归直线方程为![]() ,
,
要使月销售量不低于12万件,则有![]() ,解得
,解得![]() ,
,
∴月销售单价的最大值为8.75元;
(Ⅱ)由题意可得销售单价共有5个,其中使得月销售量不低于10万件的有2个,记为![]() ,月销售量不低于8万件不足10万件的有1个,记为
,月销售量不低于8万件不足10万件的有1个,记为![]() ,月销售量低于8万件的有2个,记为
,月销售量低于8万件的有2个,记为![]() ,从中任取2个有:
,从中任取2个有:![]() 共10个,抽到的产品含有月销量量不低于10万件的有7个,∴所求概率为
共10个,抽到的产品含有月销量量不低于10万件的有7个,∴所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有一面积为12000平方米的三角形地块![]() ,其中边
,其中边![]() 长为200米,现计划建一个如图所示的长方形停车场
长为200米,现计划建一个如图所示的长方形停车场![]() ,停车场的四个顶点都在
,停车场的四个顶点都在![]() 的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设
的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设![]() 米,建设工程的总费用为
米,建设工程的总费用为![]() 元.
元.
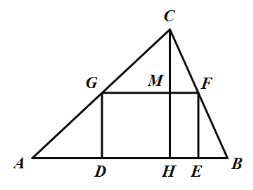
(1)求![]() 关于
关于![]() 的函数表达式:
的函数表达式:
(2)求停车场面积最大时![]() 的值,并求此时的工程总费用.
的值,并求此时的工程总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() ,
,![]() ,
,![]() 等8人中选出5人排成一排.
等8人中选出5人排成一排.
(1)![]() 必须在内,有多少种排法?
必须在内,有多少种排法?
(2)![]() ,
,![]() ,
,![]() 三人不全在内,有多少种排法?
三人不全在内,有多少种排法?
(3)![]() ,
,![]() ,
,![]() 都在内,且
都在内,且![]() ,
,![]() 必须相邻,
必须相邻,![]() 与
与![]() ,
,![]() 都不相邻,都多少种排法?
都不相邻,都多少种排法?
(4)![]() 不允许站排头和排尾,
不允许站排头和排尾,![]() 不允许站在中间(第三位),有多少种排法?
不允许站在中间(第三位),有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1.记
的首项为1.记![]() .
.
(1)若![]() 为常数列,求
为常数列,求![]() 的值:
的值:
(2)若![]() 为公比为2的等比数列,求
为公比为2的等比数列,求![]() 的解析式:
的解析式:
(3)是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立?若存在,求出数列
都成立?若存在,求出数列![]() 的通项公式:若不存在,请说明理由.
的通项公式:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
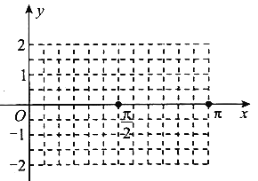
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在
在![]() 上的图象;
上的图象;
(2)若![]() 为奇函数,求
为奇函数,求![]() ;
;
(3)在(2)的前提下,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 上的单调递增区间.
上的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com