
设![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且![]() 为它的右准线。
为它的右准线。
(Ⅰ)、求椭圆的方程;
(Ⅱ)、设![]() 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() 的点
的点![]() ,证明点
,证明点![]() 在以
在以![]() 为直径的圆内。
为直径的圆内。
(此题不要求在答题卡上画图)
解:(Ⅰ)依题意得 a=2c,![]() =4,解得a=2,c=1,从而b=
=4,解得a=2,c=1,从而b=![]() .
.
故椭圆的方程为 ![]() .
.
(Ⅱ)解法1:由(Ⅰ)得A(-2,0),B(2,0).设M![]() .
.
∵M点在椭圆上,∴y0=![]() (4-x02). ………………… ①
(4-x02). ………………… ①
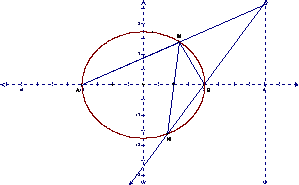
又点M异于顶点A、B,∴-2<x0<2,由P、A、M三点共线可以得
P(4,![]() ).
).
从而![]() =(x0-2,y0),
=(x0-2,y0),
![]() =(2,
=(2,![]() ).
).
∴![]() ?
?![]() =2x0-4+
=2x0-4+![]() =
=![]() (x02-4+3y02). … …………… ②
(x02-4+3y02). … …………… ②
将①代入②,化简得![]() ?
?![]() =
=![]() (2-x0).
(2-x0).
∵2-x0>0,∴![]() ?
?![]() >0,则∠MBP为锐角,从而∠MBN为钝角,
>0,则∠MBP为锐角,从而∠MBN为钝角,
故点B在以MN为直径的圆内。
解法2:由(Ⅰ)得A(-2,0),B(2,0).设M(x1,y1),N(x2,y2),
则-2< x1<2,-2< x2<2,又MN的中点Q的坐标为(![]() ,
,![]() ),
),
依题意,计算点B到圆心Q的距离与半径的差
![]() -
-![]() =(
=(![]() -2)2+(
-2)2+(![]() )2-
)2-![]() [( x1-x2)2+(y1-y2)2]
[( x1-x2)2+(y1-y2)2]
=(x1-2) (x2-2)+y1y2 ③
又直线AP的方程为y=![]() ,直线BP的方程为y=
,直线BP的方程为y=![]() ,
,
而点两直线AP与BP的交点P在准线x=4上,
∴![]() ,即y2=
,即y2=![]() ④
④
又点M在椭圆上,则![]() ,即
,即![]() ⑤
⑤
于是将④、⑤代入③,化简后可得![]() -
-![]() =
=![]() .
.
从而,点B在以MN为直径的圆内。


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2014届浙江省高二下学期期中文科数学试卷(解析版) 题型:选择题
设 分别为椭圆
分别为椭圆 的左、右焦点,点A,B在椭圆上,若
的左、右焦点,点A,B在椭圆上,若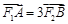 ,
,
则点A的坐标是( )
A. B.
B. C.
C.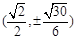 D.
D.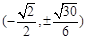
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉市武昌区高三五月调研理科数学试卷(解析版) 题型:选择题
设 分别为椭圆
分别为椭圆 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 的点
的点 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是
A.
 B.
B. C.
C.
 D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第四次月考理科数学试卷 题型:解答题
设 ,
, 分别为椭圆
分别为椭圆
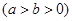 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 的倾斜角为
的倾斜角为 ,
, 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的焦距;
的焦距;
(2)如果 ,求椭圆
,求椭圆 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷十二文科数学 题型:解答题
设 分别为椭圆
分别为椭圆 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且 为它的右准线.
为它的右准线.
(Ⅰ)求椭圆的方程;
(Ⅱ)设 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线 分别与椭圆相交于异于
分别与椭圆相交于异于 的点
的点 ,证明点
,证明点 在以
在以 为直径的圆内.
为直径的圆内.
(此题不要求在答题卡上画图)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com