Question

13．在矩形ABCD中，AB=1，AD=$\sqrt{3}$，F为AC上一点，且满足${\overrightarrow{AB}}^{2}={\overrightarrow{AF}}^{2}+\overrightarrow{BF}•\overrightarrow{FD}$，则$\overrightarrow{BD}•\overrightarrow{BF}$=（　　）

• A． 0
• B． $\frac{1}{2}$
• C． 1
• D． $\frac{3}{2}$

Answer 1

分析 建立平面直角坐标系，代入坐标计算．

解答 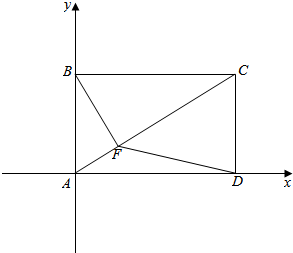解：以AD为x轴，以AB为y轴建立平面直角坐标系，如图．
∴A（0，0），B（0，1），C（$\sqrt{3}$，1），D（$\sqrt{3}$，0）．设F（a，$\frac{a}{\sqrt{3}}$），则$\overrightarrow{AF}$=（a，$\frac{a}{\sqrt{3}}$），$\overrightarrow{BF}$=（a，$\frac{a}{\sqrt{3}}-1$），
$\overrightarrow{FD}$=（$\sqrt{3}$-a，-$\frac{a}{\sqrt{3}}$）．
∵${\overrightarrow{AB}}^{2}={\overrightarrow{AF}}^{2}+\overrightarrow{BF}•\overrightarrow{FD}$，
∴1=a²+$\frac{{a}^{2}}{3}$+a（$\sqrt{3}$-a）-$\frac{a}{\sqrt{3}}$（$\frac{a}{\sqrt{3}}-1$）．解得a=$\frac{\sqrt{3}}{4}$．
∴$\overrightarrow{BD}•\overrightarrow{BF}$=（$\sqrt{3}$，-1）•（$\frac{\sqrt{3}}{4}$，-$\frac{3}{4}$）=$\sqrt{3}×\frac{\sqrt{3}}{4}$+1×$\frac{3}{4}$=$\frac{3}{2}$．
故选D．

点评 本题考查了平面向量在几何中的应用，建立平面直角坐标系是解题的常用方法．