
【题目】已知![]() (
(![]() ).
).
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)若f(x)是偶函数,求k的值;
(3)在(2)条件下,设![]() ,若函数
,若函数![]() 与
与![]() 的图象有公共点,求实数b的取值范围.
的图象有公共点,求实数b的取值范围.
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮.某公司研发的![]() ,
,![]() 两种芯片都已经获得成功.该公司研发芯片已经耗费资金
两种芯片都已经获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产.经市场调查与预测,生产
千万元,现在准备投入资金进行生产.经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() ,其图像如图所示.
,其图像如图所示.

(1)试分别求出生产![]() ,
,![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)的函数关系式;
(千万元)的函数关系式;
(2)如果公司只生产一种芯片,生产哪种芯片毛收入更大?
(3)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() ,
,![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所过利润,当
表示公司所过利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于任意的
,对于任意的![]()
![]() ,都有
,都有![]() , 当
, 当![]() 时,
时,![]() ,且
,且![]() .
.
( I ) 求![]() 的值;
的值;
(II) 当![]() 时,求函数
时,求函数![]() 的最大值和最小值;
的最大值和最小值;
(III) 设函数![]() ,判断函数g(x)最多有几个零点,并求出此时实数m的取值范围.
,判断函数g(x)最多有几个零点,并求出此时实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 对于
对于![]() 恒成立,试问是否存在实数
恒成立,试问是否存在实数![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的![]() 件产品作为样本,称出它们的重量(单位:克),重量的分组区间为
件产品作为样本,称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() ,…,
,…,![]() ,由此得到样本的频率分布方图,如图所示.
,由此得到样本的频率分布方图,如图所示.
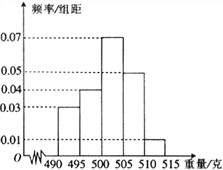
(1)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为取到重量超过
为取到重量超过![]() 克的产品件数,求
克的产品件数,求![]() 的概率;
的概率;
(2)从上述![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为取到重量超过
为取到重量超过![]() 克的产品件数,求
克的产品件数,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | _______ | _______ | 80 |
年龄大于50岁 | 10 | _______ | _______ |
合计 | _______ | 70 | 100 |
(1)根据已知数据,把表格填写完整;
(2)是否有95%的把握认为年龄与支持申办奥运有关?
附表:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.814 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}前n项和为Sn , 且满足S3= ![]() ,a6 , 3a5 , a7成等差数列. (Ⅰ)求数列{an}的通项公式;
,a6 , 3a5 , a7成等差数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列bn= ![]() ,且数列bn的前n项的和Tn , 试比较Tn与
,且数列bn的前n项的和Tn , 试比较Tn与 ![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com