
分析 若命题ρ:$\sqrt{1-sin2x}$=sinx-cosx为真,则sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$)≥0,解三角不等式可得x的取值范围.
解答 解:若$\sqrt{1-sin2x}$=$\sqrt{{{sin}^{2}x-2sinx•cosx+cos}^{2}x}$=$\sqrt{{(sinx-cosx)}^{2}}$=|sinx-cosx|=sinx-cosx,
则sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$)≥0,
则x-$\frac{π}{4}$∈[2kπ,π+2kπ],(k∈Z),
∴x∈[$\frac{π}{4}$+2kπ,$\frac{5π}{4}$+2kπ],(k∈Z)
点评 本题以命题的真假判断与应用为载体,考查了二倍角公式,指数的运算性质,和差角公式,三角函数的定义,难度中档.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:选择题
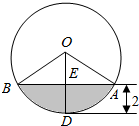 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )| A. | 4-$\frac{3\sqrt{3}}{4π}$ | B. | 2-$\frac{3\sqrt{3}}{16π}$ | C. | 3-$\frac{9\sqrt{3}}{4π}$ | D. | 3-$\frac{9\sqrt{3}}{16π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
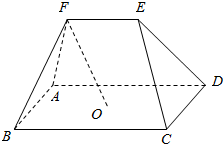 如图,在五面体ABCDE中,点O是平行四边形ABCD的对角线的交点,棱$EF\underline{\underline{∥}}\frac{1}{2}BC$
如图,在五面体ABCDE中,点O是平行四边形ABCD的对角线的交点,棱$EF\underline{\underline{∥}}\frac{1}{2}BC$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com