
【题目】唐诗是中国文学的瑰宝.为了研究计算机上唐诗分类工作中检索关键字的选取,某研究人员将唐诗分成7大类别,并从《全唐诗》48900多篇唐诗中随机抽取了500篇,统计了每个类别及各类别包含“花”、“山”、“帘”字的篇数,得到下表:
爱情婚姻 | 咏史怀古 | 边塞战争 | 山水田园 | 交游送别 | 羁旅思乡 | 其他 | 总计 | |
篇数 | 100 | 64 | 55 | 99 | 91 | 73 | 18 | 500 |
含“山”字的篇数 | 51 | 48 | 21 | 69 | 48 | 30 | 4 | 271 |
含“帘”字的篇数 | 21 | 2 | 0 | 0 | 7 | 3 | 5 | 38 |
含“花”字的篇数 | 60 | 6 | 14 | 17 | 32 | 28 | 3 | 160 |
(1)根据上表判断,若从《全唐诗》含“山”字的唐诗中随机抽取一篇,则它属于哪个类别的可能性最大,属于哪个类别的可能性最小,并分别估计该唐诗属于这两个类别的概率;
(2)已知检索关键字的选取规则为:
①若有超过95%的把握判断“某字”与“某类别”有关系,则“某字”为“某类别”的关键字;
②若“某字”被选为“某类别”关键字,则由其对应列联表得到的![]() 的观测值越大,排名就越靠前;
的观测值越大,排名就越靠前;
设“山”“帘”“花”和“爱情婚姻”对应的![]() 观测值分别为
观测值分别为![]() ,
,![]() ,
,![]() .已知
.已知![]() ,
,![]() ,请完成下面列联表,并从上述三个字中选出“爱情婚姻”类别的关键字并排名.
,请完成下面列联表,并从上述三个字中选出“爱情婚姻”类别的关键字并排名.
属于“爱情婚姻”类 | 不属于“爱情婚姻”类 | 总计 | |
含“花”字的篇数 | |||
不含“花”的篇数 | |||
总计 |
附: ,其中
,其中![]() .
.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
【答案】(1)该唐诗属于“山水田园”类别的可能性最大,属于“其他”类别的可能性最小;属于“山水田园”类别的概率约为![]() ;属于“其他”类别的概率约为
;属于“其他”类别的概率约为![]() (2)填表见解析;选择“花”,“帘”作为“爱情婚姻”类别的关键字,且排序为“花”,“帘”
(2)填表见解析;选择“花”,“帘”作为“爱情婚姻”类别的关键字,且排序为“花”,“帘”
【解析】
(1)根据统计图表算出频率,比较大小即可判断;
(2)根据统计图表完成列联表,算出![]() 观测值,查表判断.
观测值,查表判断.
(1)由上表可知,
该唐诗属于“山水田园”类别的可能性最大,属于“其他”类别的可能性最小
属于“山水田园”类别的概率约为![]() ;属于“其他”类别的概率约为
;属于“其他”类别的概率约为![]() ;
;
(2)列联表如下:
属于“爱情婚姻”类 | 不属于“爱情婚姻”类 | 共计 | |
含“花”的篇数 | 60 | 100 | 160 |
不含“花”的篇数 | 40 | 300 | 340 |
共计 | 100 | 400 | 500 |
计算得:![]() ;
;
因为![]() ,
,![]() ,所以有超过95%的把握判断“花”字和“帘”字均与“爱情婚姻”有关系,故“花”和“帘”是“爱情婚姻”的关键字,而“山”不是;
,所以有超过95%的把握判断“花”字和“帘”字均与“爱情婚姻”有关系,故“花”和“帘”是“爱情婚姻”的关键字,而“山”不是;
又因为![]() ,故选择“花”,“帘”作为“爱情婚姻”类别的关键字,且排序为“花”,“帘”.
,故选择“花”,“帘”作为“爱情婚姻”类别的关键字,且排序为“花”,“帘”.


科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,已知点
中,已知点![]() 在直线
在直线![]() 上运动,则下列四个命题中:①三棱锥
上运动,则下列四个命题中:①三棱锥![]() 的体积不变;②
的体积不变;②![]() ;③当
;③当![]() 为
为![]() 中点时,二面角
中点时,二面角![]() 的余弦值为
的余弦值为![]() ;④若正方体的棱长为2,则
;④若正方体的棱长为2,则![]() 的最小值为
的最小值为![]() ;其中说法正确的是____________(写出所有说法正确的编号)
;其中说法正确的是____________(写出所有说法正确的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R)的导函数为
R)的导函数为![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的两个不同的零点.
的两个不同的零点.
(1)证明:![]() ;
;
(2)当b=0时,若对任意x>0,不等式![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)求关于x的方程![]() 的实根的个数.
的实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月![]() 、
、![]() 两种移动支付方式的使用情况,从全校学生中随机抽取了
两种移动支付方式的使用情况,从全校学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 、
、![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 和仅使用
和仅使用![]() 的学生的支付金额分布情况如下:
的学生的支付金额分布情况如下:
支付金额(元) 支付方式 |
|
| 大于 |
仅使用 |
|
|
|
仅使用 |
|
|
|
(1)从样本仅使用![]() 和仅使用
和仅使用![]() 的学生中各随机抽取
的学生中各随机抽取![]() 人,以
人,以![]() 表示这
表示这![]() 人中上个月支付金额大于
人中上个月支付金额大于![]() 元的人数,求
元的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用![]() 的学生中,随机抽查
的学生中,随机抽查![]() 人,发现他们本月的支付金额都大于
人,发现他们本月的支付金额都大于![]() 元.根据抽查结果,能否认为样本仅使用
元.根据抽查结果,能否认为样本仅使用![]() 的学生中本月支付金额大于
的学生中本月支付金额大于![]() 元的人数有变化?说明理由.
元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 满足:
满足:![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 中的项都在数列
中的项都在数列![]() 中;
中;
(3)将数列![]() 、
、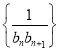 的项按照:当
的项按照:当![]() 为奇数时,
为奇数时,![]() 放在前面:当
放在前面:当![]() 为偶数时,
为偶数时,![]() 放在前面进行“交叉排列”,得到一个新的数列:
放在前面进行“交叉排列”,得到一个新的数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…这个新数列的前
,…这个新数列的前![]() 和为
和为![]() ,试求
,试求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为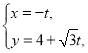 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线和曲线
分别交直线和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com