
 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.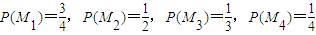 ,
,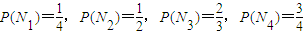 .
.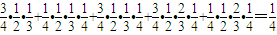
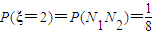 ,
,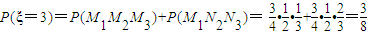 ,
, -
- =
=
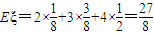 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(山东卷)解析版(理) 题型:解答题
某学校举行知识竞赛,第一轮选拔共设有A、B、C、D四个问题,规则如下:
①每位参加者计分器的初初始分均为10分,答对问题A、B、C、D分别加1分、2分、3分、6分,答错任一题减2分
②每回答一题,计分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③每位参加者按问题A、B、C、D顺序作答,直至答题结束.
假设甲同学对问题A、B、C、D回答正确的概率依次为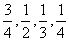 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用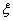 表示甲内当家本轮答题结束时答题的个数,求
表示甲内当家本轮答题结束时答题的个数,求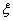 的分布列和数学期望E
的分布列和数学期望E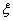 .
.
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省孝感市安陆一中高二(上)期末复习综合测试卷(1)(必修3和选修2-3)(解析版) 题型:解答题
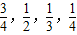 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.查看答案和解析>>
科目:高中数学 来源:2010年山东省高考数学试卷(理科)(解析版) 题型:解答题
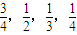 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com