Question

【题目】已知椭圆C： （a＞b＞0）经过点（2， ）且离心率等于 ，点A，B分别为椭圆C的左右顶点，点P在椭圆C上．
（1）求椭圆C的方程；
（2）M，N是椭圆C上非顶点的两点，满足OM∥AP，ON∥BP，求证：三角形MON的面积是定值．

Answer 1

【答案】
（1）解：椭圆C： （a＞b＞0）经过点（2， ）且离心率等于 ，

可得 = ，即： ， ，解得a2=8，b2=4，

所求椭圆方程为：

（2）证明：由题意M，N是椭圆C上非顶点的两点，

且AP∥OM，BP∥ON，设P（2 cosθ，2sinθ）

则直线AP，BP斜率必存在且不为0，

又由已知kAPkBP= = =- ．

因为AP∥OM，BP∥ON，所以kOMkON=-

设直线MN的方程为x=my+t，代入椭圆方程 ，

得（2+m2）y2+2mty+t2﹣8=0…①，

设M，N的坐标分别为M（x1，y1），N（x2，y2），

则y1+y2=﹣ ，y1y2= ，x1x2=

m2y1y2+mt（y1+y2）+t2= ，

所以kOMkON= = =﹣ ，得t2=2m2+4，

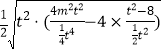又S△MON= |t||y1﹣y2|= = = = =2 ，

即△MON的面积为定值2

【解析】（1）利用椭圆的离心率以及椭圆结果的点，求出长半轴与短半轴的长，即可得到椭圆方程；（2）求出kAPkBP=﹣ ，设直线MN的方程为x=my+t，代入椭圆方程，利用kOMkON=﹣ ，推出t2=2m2+4，利用三角形的面积公式，化简求解即可推出结论．
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：，焦点在y轴：．