
����Ŀ��ij��Ϊ���������������ˮ������������ˮʵ�ж�������ʽˮ�ۼ����취���������£���һ���ݣ�ÿ����������ˮ��������12�֣��۸�Ϊ4Ԫ/�֣��ڶ����ݣ�ÿ����������ˮ������12�֣��������ֵļ۸�Ϊ8Ԫ/��.Ϊ���˽�ȫ�о�������ˮ���ķֲ������ͨ�����������100�����������ˮ������λ���֣��������ݰ���![]() ��
�� ![]() ������
������ ![]() �ֳ�8�飬�Ƴ�����ͼ1��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�ֳ�8�飬�Ƴ�����ͼ1��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
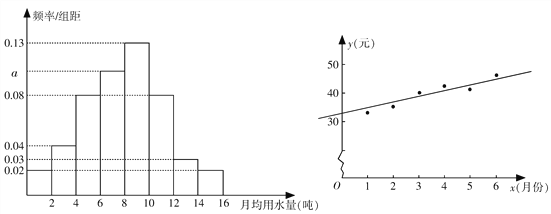
(ͼ1) (ͼ2)
������Ƶ�ʷֲ�ֱ��ͼ����ĸ![]() ��ֵ����������Ƶ�ʣ�
��ֵ����������Ƶ�ʣ�
����ͨ��Ƶ�ʷֲ�ֱ��ͼ�����Ƹ��о���ÿ�µ���ˮ������λ��![]() ��ֵ��������λС������
��ֵ��������λС������
������ͼ2�Ǹ��о�����ij2016��1��6�·ݵ�����ˮ��![]() ��Ԫ�����·�
��Ԫ�����·�![]() ��ɢ��ͼ������ϵ����Իع鷽����
��ɢ��ͼ������ϵ����Իع鷽����![]() . ����ij2016��1��7�·�ˮ����֧��Ϊ312Ԫ���Թ�����ij7�·ݵ���ˮ����.
. ����ij2016��1��7�·�ˮ����֧��Ϊ312Ԫ���Թ�����ij7�·ݵ���ˮ����.
���𰸡�����![]() ����
����![]() 8.15;����
8.15;����![]() ��.
��.
��������������������������ݸ����������Ϊ![]() �ɵý��������������
�ɵý��������������![]() �����������
�����������![]() �з��̿ɵý��������������ǰ������ƽ����ˮ�������ûع鷽�̹����ǰ������ƽ�����ã��ܷ��ü�ȥǰ�����µķ��úͼ��ɵý��.
�з��̿ɵý��������������ǰ������ƽ����ˮ�������ûع鷽�̹����ǰ������ƽ�����ã��ܷ��ü�ȥǰ�����µķ��úͼ��ɵý��.
�������������![]()
��![]()
�������Ƶ��Ϊ�� ![]()
������Ϊ![]()
����![]() 8.15
8.15
����![]() ����
����![]()
��![]()
������ij7�·ݵ���ˮ��Ϊ![]()
����ij7�·ݵ���ˮ����![]() �֣�
�֣�
��![]()
��![]() ��
�� ![]() .
.
����ij7�·ݵ���ˮ����![]() ��.
��.


 ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ������
������![]() ��ǰ
��ǰ![]() ��ͣ�
��ͣ� ![]() .
.
��1����֤������![]() �ǵȲ����У�����
�ǵȲ����У�����![]() ��ͨ�
��ͨ�
��2����![]() ��������
��������![]() ��ǰ
��ǰ![]() ���
���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�ÿ����������ģ�͡�����ģ�͡�С����ģ����������߹�100������֪����һ������ģ����5���ӣ�����һ������ģ����7���ӣ�����һ��С����ģ����4������������һ������ģ�Ϳɻ�����8Ԫ������һ������ģ�Ϳɻ�����9Ԫ������һ��С����ģ�Ϳɻ�����6Ԫ����������ʱ�䲻����10Сʱ���ù�˾����������������ʹÿ���������������������______________Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������⣨��Ե�����ָ�����г�����ֱ�ߵ�һ���⣩�ֱ���ȣ��ҳ��ֱ�Ϊ![]() ������
������![]() �����������������ֵΪ
�����������������ֵΪ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��������
��������![]() ��������
���У�����![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ����
����![]() .������
.������![]() ��������
��������![]() �����������ε��ܳ�Ϊ6��
�����������ε��ܳ�Ϊ6��
(��) ��![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
(��) ��б��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ���㣬��
���㣬��![]() ����
����![]() λ��ֱ��
λ��ֱ��![]() ������ʱ��֤����
������ʱ��֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1��������![]() ������
������![]() �ϵ�����������
�ϵ�����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���У���
���У���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD��A1B1C1D1���ⳤΪ8cm��M��N��P�ֱ���AB��A1D1 �� BB1���е㣮
��1��������M��N��P�����ƽ����ƽ��A1B1C1D1�Ľ����Լ���ƽ��BB1C1C�Ľ��ߣ�
��2�����M��N��P�����ƽ����B1C1����Q����PQ�ij���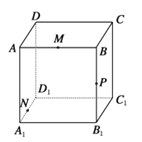
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ���Լ���Ϊԭ�㣬����Ϊ
���Լ���Ϊԭ�㣬����Ϊ![]() ��������ᣬ����ƽ��ֱ������ϵ��ֱ��
��������ᣬ����ƽ��ֱ������ϵ��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ��������
��������
��1���ж�ֱ��![]() ������
������![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2����ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ����ֱ��
����ֱ��![]() ��б�ʣ�
��б�ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c��d��E��֤�����в���ʽ��
��1����a2+b2����c2+d2���ݣ�ac+bd��2��
��2��a2+b2+c2��ab+bc+ca��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com