
【题目】如图,已知矩形 ![]() 所在平面与等腰直角三角形
所在平面与等腰直角三角形 ![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() ,
, ![]() 为线段
为线段 ![]() 的中点.
的中点.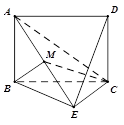
(Ⅰ)证明: ![]() ;
;
(Ⅱ)求 ![]() 与平面
与平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
【答案】解:(Ⅰ) 因为 ![]() ,所以
,所以 ![]() ,故
,故 ![]() .因为
.因为 ![]() ,所以
,所以 ![]() ,故
,故 ![]() .
.
因为 ![]() ,
, ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() .
.
所以 ![]() .
.
(Ⅱ)如图,将几何体 ![]() 补成三棱柱
补成三棱柱 ![]() ,
,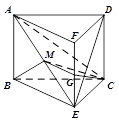
设 ![]() 的中点为
的中点为 ![]() ,连结
,连结 ![]() .
.
因为 ![]() ,所以
,所以 ![]() .
.
因此 ![]() 为
为 ![]() 与平面
与平面 ![]() 所成的角.
所成的角.
不妨设 ![]() ,则
,则 ![]() ,因此
,因此 ![]() ,
, ![]() ,
, ![]() ,故
,故 ![]() ,
,
所以 ![]() 与平面
与平面 ![]() 所成的角的余弦值为
所成的角的余弦值为 ![]() .
.
【解析】(Ⅰ)由已知推导出AB⊥EC,EC⊥BM,AE⊥BM,由此能证明BM⊥平面AEC.
(Ⅱ)将几何体ABCDE补成三棱柱AFD-BEC,设EF的中点为G,连结MG,GC,推导出∠MCG为MC与平面DEC所成的角,由此能求出MC与平面DEC所成的角的余弦值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() 为参数,
为参数, ![]() ). 以坐标原点为极点,
). 以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)设 ![]() 是曲线
是曲线 ![]() 上的一个动点,当
上的一个动点,当 ![]() 时,求点
时,求点 ![]() 到直线
到直线 ![]() 的距离的最大值;
的距离的最大值;
(2)若曲线 ![]() 上所有的点均在直线
上所有的点均在直线 ![]() 的右下方,求
的右下方,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网店和实体店各有利弊,两者的结合将在未来一段时期内,成为商业的一个主要发展方向.某品牌行车记录仪支架销售公司从 ![]() 年
年 ![]() 月起开展网络销售与实体店体验安装结合的销售模式.根据几个月运营发现,产品的月销量
月起开展网络销售与实体店体验安装结合的销售模式.根据几个月运营发现,产品的月销量 ![]() 万件与投入实体店体验安装的费用
万件与投入实体店体验安装的费用 ![]() 万元之间满足
万元之间满足 ![]() 函数关系式.已知网店每月固定的各种费用支出为
函数关系式.已知网店每月固定的各种费用支出为 ![]() 万元,产品每
万元,产品每 ![]() 万件进货价格为
万件进货价格为 ![]() 万元,若每件产品的售价定为“进货价的
万元,若每件产品的售价定为“进货价的 ![]() ”与“平均每件产品的实体店体验安装费用的一半”之和,则该公司最大月利润是万元.
”与“平均每件产品的实体店体验安装费用的一半”之和,则该公司最大月利润是万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(1+x)+mln(1-x)是偶函数,则( )
A.m=1,且f(x)在(0,1)上是增函数
B.m=1,且f(x)在(0,1)上是减函数
C.m=-1,且f(x)在(0,1)上是增函数
D.m=-1,且f(x)在(0,1)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺 .问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”. 就是说:圆堡瑽(圆柱体)的体积为 ![]() (底面圆的周长的平方
(底面圆的周长的平方 ![]() 高),则由此可推得圆周率
高),则由此可推得圆周率 ![]() 的取值为( )
的取值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的部分图像如图所示,将
的部分图像如图所示,将 ![]() 的图象向右平移
的图象向右平移 ![]() 个单位长度后得到函数
个单位长度后得到函数 ![]() 的图象.
的图象.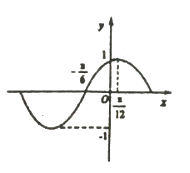
(1)求函数 ![]() 的解折式;
的解折式;
(2)在 ![]() 中,角
中,角 ![]() 满足
满足 ![]() ,且其外接圆的半径
,且其外接圆的半径 ![]() ,求
,求 ![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com