
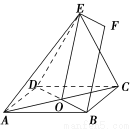
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=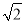 EF.
EF.
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
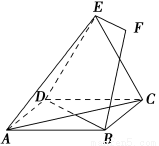
(1)详见解析, (2) 详见解析.
【解析】
试题分析:(1) 证明线面平行,需先证线线平行. 正方形ABCD中,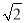 BO=AB,又因为AB=
BO=AB,又因为AB=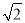 EF,∴BO=EF,又因为EF∥BD,∴EFBO是平行四边形,∴BF∥EO,又∵BF?平面ACE,EO?平面ACE,∴BF∥平面ACE.列线面平行判定定理的条件必须要全面. (2)证明线线垂直,一般利用线面垂直进行转化.条件为面面垂直,所以先由面面垂直性质定理转化为线面垂直:正方形ABCD中,AC⊥BD,又因为正方形ABCD和三角形ACE所在的平面互相垂直,BD?平面ABCD,平面ABCD∩平面ACE=AC,∴BD⊥平面ACE,∵EO?平面ACE,∴BD⊥EO,∵EO∥BF,∴BF⊥BD.
EF,∴BO=EF,又因为EF∥BD,∴EFBO是平行四边形,∴BF∥EO,又∵BF?平面ACE,EO?平面ACE,∴BF∥平面ACE.列线面平行判定定理的条件必须要全面. (2)证明线线垂直,一般利用线面垂直进行转化.条件为面面垂直,所以先由面面垂直性质定理转化为线面垂直:正方形ABCD中,AC⊥BD,又因为正方形ABCD和三角形ACE所在的平面互相垂直,BD?平面ABCD,平面ABCD∩平面ACE=AC,∴BD⊥平面ACE,∵EO?平面ACE,∴BD⊥EO,∵EO∥BF,∴BF⊥BD.
证明 (1)AC与BD交于O点,连接EO.
正方形ABCD中,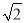 BO=AB,又因为AB=
BO=AB,又因为AB=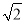 EF,
EF,
∴BO=EF,又因为EF∥BD,
∴EFBO是平行四边形,
∴BF∥EO,又∵BF?平面ACE,EO?平面ACE,
∴BF∥平面ACE 7分
(2)正方形ABCD中,AC⊥BD,又因为正方形ABCD和三角形ACE所在的平面互相垂直,BD?平面ABCD,平面ABCD∩平面ACE=AC,
∴BD⊥平面ACE,∵EO?平面ACE,
∴BD⊥EO,∵EO∥BF,∴BF⊥BD. 14分
考点:线面平行判定定理,面面垂直性质定理,


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源:2013-2014学年江苏省盐城市高三第三次模拟考试数学试卷(解析版) 题型:解答题
若数列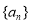 满足
满足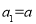 且
且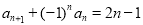 (其中
(其中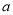 为常数),
为常数),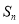 是数列
是数列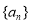 的前
的前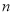 项和,数列
项和,数列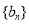 满足
满足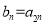 .
.
(1)求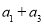 的值;
的值;
(2)试判断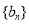 是否为等差数列,并说明理由;
是否为等差数列,并说明理由;
(3)求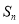 (用
(用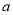 表示).
表示).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练理科数学试卷(解析版) 题型:填空题
若中心在原点、焦点在坐标轴上的双曲线的一条渐近线方程为 ,则此双曲线的离心率为
,则此双曲线的离心率为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com