
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上.
的图像上.
(1)证明:当![]() 时,
时,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() 为数列
为数列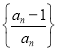 的前n项的积,若不等式
的前n项的积,若不等式![]() 对一切
对一切![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)证明见解析; (2)![]() (3)
(3)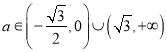
【解析】
(1)根据点在函数图像上,代入点坐标,化简后结合![]() 即可证明.
即可证明.
(2)根据(1)所得递推公式,递推作差后可得奇偶项分别为等差数列,根据![]() 和公差即可求得通项公式.
和公差即可求得通项公式.
(3)根据![]() 为数列
为数列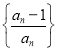 ,代入
,代入![]() 的通项公式求得
的通项公式求得![]() 的表达式,构造函数
的表达式,构造函数![]() ;代入
;代入![]() 的通项公式求得函数
的通项公式求得函数![]() ,根据恒成立求得
,根据恒成立求得![]() 即可.通过
即可.通过![]() 的单调性求得
的单调性求得![]() ,代入解不等即可得实数a的取值范围.
,代入解不等即可得实数a的取值范围.
(1)证明: 因为对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上
的图像上
所以![]() ,化简可得
,化简可得![]()
当![]() 时,
时, ![]()
两式相减可得![]()
即![]() (
(![]() )
)
原式得证.
(2)由(1)可知![]()
所以![]()
![]()
两式相减,可得![]()
所以数列![]() 的奇数项公差为4的等差数列,偶数项公差为4的等差数列.
的奇数项公差为4的等差数列,偶数项公差为4的等差数列.
由(1)可知![]()
则当![]() 时,
时, ![]() 求得
求得![]()
则当![]() 时,
时, ![]() ,即
,即![]() 求得
求得![]()
所以当![]() 为奇数时,
为奇数时, ![]()
所以当![]() 为偶数时,
为偶数时, ![]()
综上可知数列![]() 的通项公式为
的通项公式为![]()
(3)因为![]()
所以![]()
所以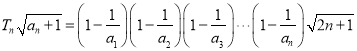
又因为![]()
所以![]() 对一切
对一切![]() 成立
成立
即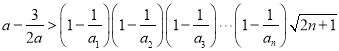 对一切
对一切![]() 成立
成立
只需满足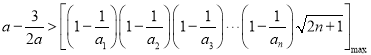 即可
即可
令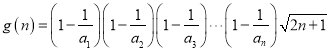
则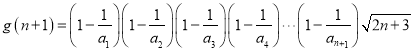
所以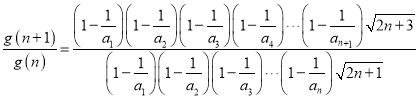

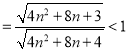
所以![]()
即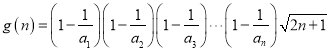 为单调递减数列
为单调递减数列
所以![]()
所以![]() 即可,化简可得
即可,化简可得
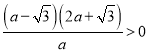
解不等式可得![]() ,或
,或![]()
故实数a的取值范围为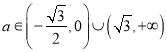


科目:高中数学 来源: 题型:
【题目】某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β

(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a表示.
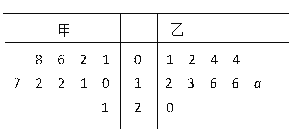
(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值,求图中a的所有可能取值;
(Ⅱ)将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设![]() ,现从所有的“阅读达人”里任取2人,求至少有1人来自甲组的概率;
,现从所有的“阅读达人”里任取2人,求至少有1人来自甲组的概率;
(Ⅲ)记甲组阅读量的方差为![]() . 若在甲组中增加一个阅读量为10的学生,并记新得到的甲组阅读量的方差为
. 若在甲组中增加一个阅读量为10的学生,并记新得到的甲组阅读量的方差为![]() ,试比较
,试比较![]() ,
,![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
(注:![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,M是椭圆C的上顶点,
,M是椭圆C的上顶点,![]() ,F2是椭圆C的焦点,
,F2是椭圆C的焦点,![]() 的周长是6.
的周长是6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过动点P(1,t)作直线交椭圆C于A,B两点,且|PA|=|PB|,过P作直线l,使l与直线AB垂直,证明:直线l恒过定点,并求此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.“若x=3,则x2﹣2x﹣3=0”的否命题是:“若x=3,则x2﹣2x﹣3≠0”
B.在△ABC中,“A>B”是“sinA>sinB”的充要条件
C.若p∧q为假命题,则p∨q一定为假命题
D.“存在x0∈R,使得ex0≤0”的否定是:不存在x0∈R,使得e![]() 0”
0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 给出下列4个命题:①当且仅当
给出下列4个命题:①当且仅当![]() 时,
时,![]() 是偶函数;②函数
是偶函数;②函数![]() 一定存在零点;③函数在区间
一定存在零点;③函数在区间![]() 上单调递减;④当
上单调递减;④当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,那么所有真命题的序号是_______.
,那么所有真命题的序号是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com