
分析 假设在椭圆上找到一点M(m,n),使点M到左准线的距离是它到两个焦点距离的比例中项.求得椭圆的焦点和左准线方程,由点到直线的距离和焦半径公式可得(m+4)2=(2+$\frac{1}{2}$m)(2-$\frac{1}{2}$m),解方程可得m,再由椭圆的范围即可判断.
解答 解:假设在椭圆上找到一点M(m,n),
使点M到左准线的距离是它到两个焦点距离的比例中项.
椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的a=2,b=$\sqrt{3}$,c=1,e=$\frac{1}{2}$,
设左、右焦点为F1(-1,0),F2(1,0),左准线为x=-4,
点M到左准线的距离为d=m+4,|MF1|=2+$\frac{1}{2}$m,|MF2|=2-$\frac{1}{2}$m,
由假设可得d2=|MF1|•|MF2|,
即(m+4)2=(2+$\frac{1}{2}$m)(2-$\frac{1}{2}$m),
即为5m2+32m+48=0,
解得m=-4或m=-$\frac{12}{5}$.
由椭圆的性质可得|m|≤2,
则m=-4或m=-$\frac{12}{5}$不成立.
故不能在椭圆上找到一点M,
使点M到左准线的距离是它到两个焦点距离的比例中项.
点评 本题考查椭圆的方程和性质,考查存在性问题的解法,同时考查运算求解能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
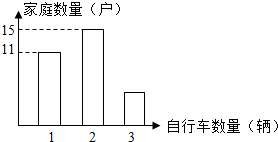 某个小区为了制订自行车棚的整修方案,进行了一次以家庭为单位的自行车数量调查.按照家庭成员的人数采用分层抽样的方法,一部分数据如表所示,其中m=2n.通过调查统计了每个家庭的自行车数量,将结果绘制成条形图,如图所示.
某个小区为了制订自行车棚的整修方案,进行了一次以家庭为单位的自行车数量调查.按照家庭成员的人数采用分层抽样的方法,一部分数据如表所示,其中m=2n.通过调查统计了每个家庭的自行车数量,将结果绘制成条形图,如图所示.| 家庭人数 | 1 | 2 | 3 | 4 | 5 |
| 家庭数量 | 6 | m | 72 | 18 | |
| 抽样数量 | 4 | n | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com