
分析 (1)由椭圆的离心率得到a,b的关系,再由$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值为-2求得a的值,则b可求,椭圆方程可求;
(2)由(1)知F1(-$\sqrt{2}$,0),F2($\sqrt{2}$,0),则斜率不存在时,用坐标分别表示出$\overrightarrow{{F}_{2}M}$,$\overrightarrow{{F}_{2}N}$,直接求得$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$;直线斜率存在时,设直线MN的方程为y=k(x+$\sqrt{2}$),代入椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,消去y得(1+2k2)x2+4$\sqrt{2}$k2x+4(k2-1)=0.利用根与系数的关系求得M,N的横纵坐标的积,把$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$转化为M,N的横坐标的和与积的形式,代入后化为关于k的函数式得答案.
解答 解:(1)由题意知,$\frac{c}{a}=\frac{\sqrt{2}}{2}$,即$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{2}$,
∴$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$,则a2=2b2,
设P(x,y),
∵$\overrightarrow{PA}$•$\overrightarrow{PB}$=(-a-x,-y)•(a-x,-y)
=${x}^{2}-{a}^{2}+{y}^{2}={x}^{2}-{a}^{2}+\frac{{a}^{2}}{2}-\frac{{x}^{2}}{2}$=$\frac{1}{2}({x}^{2}-{a}^{2})$,
∵-a≤x≤a,∴当x=0时,$(\overrightarrow{PA}•\overrightarrow{PB})_{min}=-\frac{{a}^{2}}{2}=-2$,
∴a2=4,则b2=2.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)由a2=4,b2=2,得$c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{2}$,
∴${F}_{1}(-\sqrt{2},0),{F}_{2}(\sqrt{2},0)$,
则直线斜率不存在时,
M(-$\sqrt{2}$,1),N(-$\sqrt{2}$,-1),于是$\overrightarrow{{F}_{2}M}=(-2\sqrt{2},1)$,$\overrightarrow{{F}_{2}N}$=(-2$\sqrt{2}$,-1),
∴$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$=7;
直线斜率存在时,设直线MN的方程为y=k(x+$\sqrt{2}$),代入椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,消去y得
(1+2k2)x2+4$\sqrt{2}$k2x+4(k2-1)=0.
设M(x1,y1),N(x2,y2),则${x}_{1}+{x}_{2}=-\frac{4\sqrt{2}{k}^{2}}{1+2{k}^{2}}$,${x}_{1}{x}_{2}=\frac{4({k}^{2}-1)}{1+2{k}^{2}}$,
∵$\overrightarrow{{F}_{2}M}=({x}_{1}-\sqrt{2},{y}_{1}),\overrightarrow{{F}_{2}N}=({x}_{2}-\sqrt{2},{y}_{2})$,
∴$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$=${x}_{1}{x}_{2}-\sqrt{2}({x}_{1}+{x}_{2})+2+{k}^{2}({x}_{1}+\sqrt{2})({x}_{2}+\sqrt{2})$
=$(1+{k}^{2}){x}_{1}{x}_{2}+(\sqrt{2}{k}^{2}-\sqrt{2})({x}_{1}+{x}_{2})$+2k2+2
=$(1+{k}^{2})•\frac{4({k}^{2}-1)}{1+2{k}^{2}}+\sqrt{2}({k}^{2}-1)•\frac{-4\sqrt{2}{k}^{2}}{1+2{k}^{2}}$+2k2+2
=$7-\frac{9}{1+2{k}^{2}}$.
∵1+2k2≥1,∴0<$\frac{1}{1+2{k}^{2}}$≤1
∴$7-\frac{9}{1+2{k}^{2}}$∈[-2,7),
综上知,$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$∈[-2,7].
点评 本题以向量为载体,考查椭圆的标准方程,考查向量的数量积,考查运算能力,解题时应注意分类讨论,同时正确用坐标表示向量,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | a≤-4 | B. | a≤-2 | C. | a≥-2 | D. | a>-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
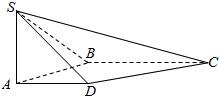 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\sqrt{n}$-$\sqrt{n-1}$ | B. | an=$\sqrt{n}$+$\sqrt{n-1}$ | C. | an=$\sqrt{n}$-$\sqrt{n+1}$ | D. | an=$\sqrt{n}$+$\sqrt{n+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com