
【题目】已知直线y=k(x﹣m)与抛物线y2=2px(p>0)交于A、B两点,O为坐标原点,OA⊥OB,OD⊥AB于D,点D在曲线x2+y2﹣4x=0上,则p= .
 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
【题目】为纪念重庆黑山谷晋升国家5A级景区五周年,特发行黑山谷纪念邮票,从2017年11月1日起开始上市.通过市场调查,得到该纪念邮票在一周内每1张的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
上市时间x天 | 1 | 2 | 6 |
市场价y元 | 5 | 2 | 10 |
(Ⅰ)分析上表数据,说明黑山谷纪念邮票的市场价y(单位:元)与上市时间x(单位:天)的变化关系,并判断y与x满足下列哪种函数关系,①一次函数;②二次函数;③对数函数,并求出函数的解析式;
(Ⅱ)利用你选取的函数,求黑山谷纪念邮票市场价最低时的上市天数及最低的价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知l1 , l2 , l3 , …ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1 , P2 , P3 , …Pn分别在直线l1 , l2 , l3 , …ln上.若 ![]() =xn
=xn ![]() +yn
+yn ![]() (n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为 .
(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,依次连接椭圆的四个顶点得到的菱形面积为4.
,依次连接椭圆的四个顶点得到的菱形面积为4.
(1)求椭圆的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,设
两点,设![]() 与
与![]() 面积之比为
面积之比为![]() (其中
(其中![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC 内部取n 个点, 将△ABC剖分为若干个小三角形(每两个小三角形或者有一个公共顶点,或者有一条公共边,或者完全没有公共点,如图所示).现将点A 染红色, 点B 染蓝色,点C 染黑色,其余n 个点的每个点也任意染上红、蓝、黑三色之一.我们称三个顶点的颜色恰为红、蓝、黑的小三角形为“特征三角形”.证明:至少有一个小三角形是特征三角形.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)上一点与它的左、右两个焦点F1 , F2的距离之和为2
(a>b>0)上一点与它的左、右两个焦点F1 , F2的距离之和为2 ![]() ,且它的离心率与双曲线x2﹣y2=2的离心率互为倒数.
,且它的离心率与双曲线x2﹣y2=2的离心率互为倒数.
(1)求椭圆的方程;
(2)如图,点A为椭圆上一动点(非长轴端点),AF1的延长线与椭圆交于点B,AO的延长线与椭圆交于点C.
①当直线AB的斜率存在时,求证:直线AB与BC的斜率之积为定值;
②求△ABC面积的最大值,并求此时直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.
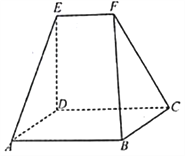
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于5.
的距离之比等于5.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为 8,求直线
所截得的线段的长为 8,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com