
��12�֣���һ��߳�Ϊ4�������θְ壬�ֶ����и���ӳ�һ�����������������С�����ĺ��Բ��ƣ�������Ӧ����ѧ֪ʶ��������ƣ��ڸְ���ĸ��Ǵ�����ȥһ��ȫ�ȵ�С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳���
��1��������������и���Ӷ��ɵij���������������ݻ� ��
��
��2�������ж����������Ƿ�����ѷ����������ǣ������һ���·�����ʹ�����˷����٣������ó������������ݻ� ��
��
��1����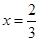 ʱ��
ʱ��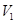 ȡ���ֵ
ȡ���ֵ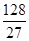 ��
��
��2��������Ʒ������£�

��ͼ�٣��������ε������Ǵ�������һ���߳�Ϊ1��С�����Σ���ͼ�ڣ������µ�С�����κ���δ�пڵ�������һ�ߵ��м䣻��ͼ�ں��ɳ���������.�º�����������������һ�����Σ���Ϊ3����Ϊ2���˳������ݻ�Ϊ6���ʵڶ��ַ�������Ҫ��.
����������������Ҫ�ǿ����˵������о������е����á������ֵ���⡣
��1����Ϊ����ȥ�����α߳�Ϊx���ӳɵij�����ĵ���߳�Ϊ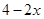 ����Ϊx��
����Ϊx��
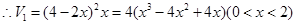 ��Ȼ���������ж������Եõ���ֵ�����������ֵ��
��Ȼ���������ж������Եõ���ֵ�����������ֵ��
��2���������ε������Ǵ�������һ���߳�Ϊ1��С�����Σ���ͼ�ڣ������µ�С�����κ���δ�пڵ�������һ�ߵ��м䣻��ͼ�ں��ɳ���������.�º�����������������һ�����Σ���Ϊ3����Ϊ2���˳������ݻ�Ϊ6���ʵڶ��ַ�������Ҫ��
��1������ȥ�����α߳�Ϊx���ӳɵij�����ĵ���߳�Ϊ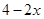 ����Ϊx��
����Ϊx��
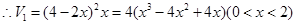 ������2�֣�
������2�֣�
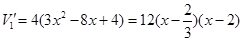 . ������3�֣�
. ������3�֣�
��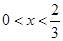 ʱ��
ʱ��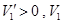 �ǹ���x����������
�ǹ���x����������
��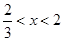 ʱ��
ʱ��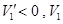 �ǹ���x�ļ�����.
�ǹ���x�ļ�����.
�൱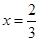 ʱ��
ʱ��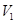 ȡ���ֵ
ȡ���ֵ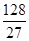 ������7�֣�
������7�֣�
��2��������Ʒ������£�

��ͼ�٣��������ε������Ǵ�������һ���߳�Ϊ1��С�����Σ���ͼ�ڣ������µ�С�����κ���δ�пڵ�������һ�ߵ��м䣻��ͼ�ں��ɳ���������.�º�����������������һ�����Σ���Ϊ3����Ϊ2���˳������ݻ�Ϊ6���ʵڶ��ַ�������Ҫ��.������12�֣�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
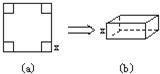 ��һ��߳�Ϊ4�������θְ壬�ֶ�������и���ӳ�һ�������������������С�����ĺ��Բ��ƣ�������Ӧ����ѧ֪ʶ����������ƣ���ͼ��a�����ڸְ���ĸ��Ǵ�����ȥһ��С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ�ΪС�����α߳�����ͼ��b����
��һ��߳�Ϊ4�������θְ壬�ֶ�������и���ӳ�һ�������������������С�����ĺ��Բ��ƣ�������Ӧ����ѧ֪ʶ����������ƣ���ͼ��a�����ڸְ���ĸ��Ǵ�����ȥһ��С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ�ΪС�����α߳�����ͼ��b�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��ɽ��ʡ������ʮ�и�����ѧ��ģ�⿼��������ѧ ���ͣ������
����С������12�֣�
��һ��߳�Ϊ4�������θְ壬�ֶ����и���ӳ�һ�����������������С�����ĺ��Բ��ƣ�.����Ӧ����ѧ֪ʶ��������ƣ��ڸְ���ĸ��Ǵ�����ȥһ��С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳�.
��1��������������и���Ӷ��ɵij���������������ݻ�V1�� ��2�������ж����������Ƿ�����ѷ����������ǣ������һ���·�����ʹ�����˷����٣������ó������������ݻ�V2��V1.
��2�������ж����������Ƿ�����ѷ����������ǣ������һ���·�����ʹ�����˷����٣������ó������������ݻ�V2��V1.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011ѧ��ɽ��ʡ�����и�����ѧ��ģ�⿼��������ѧ ���ͣ������
����С������12�֣�
��һ��߳�Ϊ4�������θְ壬�ֶ����и���ӳ�һ�����������������С�����ĺ��Բ��ƣ�.����Ӧ����ѧ֪ʶ��������ƣ��ڸְ���ĸ��Ǵ�����ȥһ��С�����Σ�ʣ�ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳�.
��1��������������и���Ӷ��ɵij���������������ݻ�V1��
��2�������ж����������Ƿ�����ѷ����������ǣ������һ���·�����ʹ�����˷����٣������ó������������ݻ�V2��V1.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010��㶫ʡ�߶���ѧ�ڵ�һ�ζο�������ѧ�� ���ͣ������
(��������14��)����һ��߳�Ϊ4�������θְ壬�ֶ����и���ӳ�һ����������������(�С�����ĺ��Բ���)������Ӧ����ѧ֪ʶ��������ƣ��ڸְ���ĸ��Ǵ�����ȥһ���߳�Ϊ
 ��С�����Σ����ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳���
��С�����Σ����ಿ��Χ��һ�������壬�ó�����ĸ���С�����εı߳���
(1)������������и���Ӷ��ɵij����������ĵ��ݻ�V1���� ��ʾ����
��ʾ����
(2)������ƣ�1���ķ���������õ��� ʱ��Vlȡ���ֵ
ʱ��Vlȡ���ֵ ��Ϊ�˲����˷����٣�����ʦ����ʵ�������������ӷ�������д���루1���ĺ��ӷ������ѣ�ʹ�����˷����٣��ݻ���Vl����Ʒ��������������������Ʒ������õ����������ݻ���
��Ϊ�˲����˷����٣�����ʦ����ʵ�������������ӷ�������д���루1���ĺ��ӷ������ѣ�ʹ�����˷����٣��ݻ���Vl����Ʒ��������������������Ʒ������õ����������ݻ���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com