
【题目】已知抛物线E:y2=2px(p>0),焦点F到准线的距离为3,抛物线E上的两个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4.线段AB的垂直平分线与x轴交于点 C.
(1)求抛物线E的方程;
(2)求△ABC面积的最大值.
【答案】(1)y2=6x(2)![]() .
.
【解析】
(1)根据抛物线定义,写出焦点坐标和准线方程,列方程即可得解;
(2)根据中点坐标表示出|AB|和点到直线的距离,得出面积,利用均值不等式求解最大值.
(1)抛物线E:y2=2px(p>0),焦点F(![]() ,0)到准线x
,0)到准线x![]() 的距离为3,可得p=3,即有抛物线方程为y2=6x;
的距离为3,可得p=3,即有抛物线方程为y2=6x;
(2)设线段AB的中点为M(x0,y0),则![]() ,
,
y0![]() ,kAB
,kAB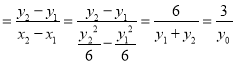 ,
,
则线段AB的垂直平分线方程为y﹣y0![]() (x﹣2),①
(x﹣2),①
可得x=5,y=0是①的一个解,所以AB的垂直平分线与x轴的交点C为定点,
且点C(5,0),由①可得直线AB的方程为y﹣y0![]() (x﹣2),即x
(x﹣2),即x![]() (y﹣y0)+2 ②
(y﹣y0)+2 ②
代入y2=6x可得y2=2y0(y﹣y0)+12,即y2﹣2y0y+2y02=0 ③,
由题意y1,y2是方程③的两个实根,且y1≠y2,
所以△=4y02﹣4(2y02﹣12)=﹣4y02+48>0,解得﹣2![]() y0<2
y0<2![]() ,
,
|AB|![]()
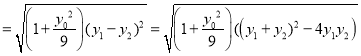
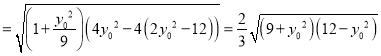 ,
,
又C(5,0)到线段AB的距离h=|CM|![]() ,
,
所以S△ABC![]()
![]()
![]()
![]() ,
,
当且仅当9+y02=24﹣2y02,即y0=±![]() ,A(
,A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
或A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )时等号成立,
)时等号成立,
所以S△ABC的最大值为![]() .
.


科目:高中数学 来源: 题型:
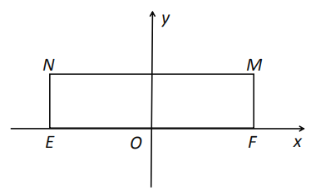
【题目】已知矩形EFMN,![]() ,
,![]() ,以EF的中点O为原点,建立如图的平面直角坐标系,若椭圆
,以EF的中点O为原点,建立如图的平面直角坐标系,若椭圆![]() 以E,F为焦点,且经过M,N两点.
以E,F为焦点,且经过M,N两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相交于A,B两点,在y轴上是否存在点C,使得△ABC为正三角形,若存在,求出l的方程;若不存在,说明理由.
相交于A,B两点,在y轴上是否存在点C,使得△ABC为正三角形,若存在,求出l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民出行,倡导低碳出行.某市公交公司推出利用支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,在推广期内采用随机优惠鼓励市民扫码支付乘车.该公司某线路公交车队统计了活动推广期第一周内使用扫码支付的情况,其中![]() (单位:天)表示活动推出的天次,
(单位:天)表示活动推出的天次,![]() (单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图.
(单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图.
表1:
x | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 |
y | 7 | 12 | 20 | 33 | 54 | 90 | 148 |

(1)由散点图分析后,可用![]() 作为该线路公交车在活动推广期使用扫码支付的人次
作为该线路公交车在活动推广期使用扫码支付的人次![]() 关于活动推出天次
关于活动推出天次![]() 的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).
的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).
表2:
|
|
| img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/08/08/88254471/SYS201908080801220877999013_ST/SYS201908080801220877999013_ST.008.png" width="67" height="40" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> |
|
|
4 | 52 | 3.5 | 140 | 2069 | 112 |
表中![]() ,
,![]() .
.
(2)推广期结束后,该车队对此期间乘客的支付情况进行统计,结果如表3.
表3:
支付方式 | 现金 | 乘车卡 | 扫码 |
频率 | 10% | 60% | 30% |
优惠方式 | 无优惠 | 按7折支付 | 随机优惠(见下面统计结果) |
统计结果显示,扫码支付中享受5折支付的频率为![]() ,享受7折支付的频率为
,享受7折支付的频率为![]() ,享受9折支付的频率为
,享受9折支付的频率为![]() .已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量
.已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量![]() 为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求
为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求![]() 的分布列和期望.
的分布列和期望.
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为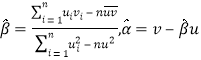 参考数据:
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种赌博每局的规则是:赌客先在标记有1,2,3,4,5的卡片中随机摸取一张,将卡片上的数字作为其赌金;随后放回该卡片,再随机摸取两张,将这两张卡片上数字之差的绝对值的1.4倍作为其奖金.若随机变量ξ1和ξ2分别表示赌客在一局赌博中的赌金和奖金,则D(ξ1)=_____,E(ξ1)﹣E(ξ2)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥V﹣ABCD中,底面ABCD是菱形,对角线AC与BD交于点O,VO⊥平面ABCD,E是棱VC的中点.
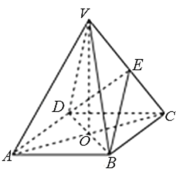
(1)求证:VA∥平面BDE;
(2)求证:平面VAC⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间4小时内生产了100根不同规格的三角钢材(单位:厘米),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
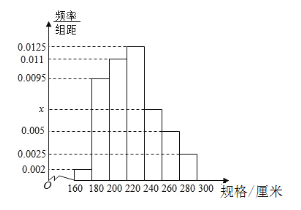
(1)求直方图中![]() 的值;
的值;
(2)求这批钢材规格的众数;
(3)在规格为![]() ,
,![]() ,
,![]() ,
,![]() 的四组钢材中,用分层抽样的方法抽取11根钢材,则在
的四组钢材中,用分层抽样的方法抽取11根钢材,则在![]() 的规格中应抽取多少根?
的规格中应抽取多少根?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com