
 如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.分析 (Ⅰ)若∠POB=θ,0<θ<π,由余弦定理将四边形OPDC的面积y表示为关于θ的函数;
(Ⅱ)当θ-$\frac{π}{3}$=$\frac{π}{2}$,即θ=$\frac{5π}{6}$时,可求四边形OPDC面积的最大值.
解答 解:(Ⅰ)在△POC中,由余弦定理,
得PC2=OP2+OC2-2OP•OC•cos θ=5-4cos θ,…(4分)
所以y=S△OPC+S△PCD
=$\frac{1}{2}$×1×2sin θ+$\frac{\sqrt{3}}{4}$×(5-4cos θ)=2sin(θ-$\frac{π}{3}$)+$\frac{5\sqrt{3}}{4}$.…(8分)
(Ⅱ)当θ-$\frac{π}{3}$=$\frac{π}{2}$,即θ=$\frac{5π}{6}$时,ymax=2+$\frac{5\sqrt{3}}{4}$.
答:四边形OPDC面积的最大值为2+$\frac{5\sqrt{3}}{4}$.…(12分)
点评 本题考查余弦定理,考查三角函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有1件次品与至多有1件正品 | B. | 恰有1件次品与恰有2件正品 | ||
| C. | 至少有1件次品与至少有1件正品 | D. | 至少有1件次品与都是正品 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不共面 | B. | 共面 | C. | 共线 | D. | 不共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
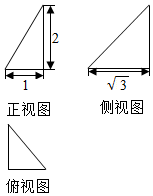 某几何体的三视图如图所示,则该几何体外接球的表面积为( )
某几何体的三视图如图所示,则该几何体外接球的表面积为( )| A. | $\frac{25π}{4}$ | B. | $\frac{25π}{8}$ | C. | 12π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com