
【题目】已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.
【答案】(1)![]() 、
、![]() ,(2)
,(2)![]() 的单调递增区间为(0,1),而
的单调递增区间为(0,1),而![]() 的单调递减区间为
的单调递减区间为![]() .(3)
.(3)![]() 的取值范围为
的取值范围为![]()
【解析】
试题分析: (1)由极值的定义和已知条件可得b﹣c=﹣3﹣c,,即b=-3;对已知函数求导,再由![]() ,列出管a,b 的等式,即可得到a的值.(2)由(1)可得到f(x)的表达式,然后对其求导,由
,列出管a,b 的等式,即可得到a的值.(2)由(1)可得到f(x)的表达式,然后对其求导,由![]() 或
或![]() ,可得到函数的单调增区间或减区间.(3)求出f(x)的最小值﹣3﹣c,已知条件式f(x)≥﹣2c2恒成立可转化为﹣3﹣c≥﹣2c2,解得c即可.
,可得到函数的单调增区间或减区间.(3)求出f(x)的最小值﹣3﹣c,已知条件式f(x)≥﹣2c2恒成立可转化为﹣3﹣c≥﹣2c2,解得c即可.
试题解析:解:(1)由题意知f(1)=﹣3﹣c,因此b﹣c=﹣3﹣c,从而b=﹣3。2分
又对f(x)求导得![]() =x3(4alnx+a+4b),
=x3(4alnx+a+4b),
由题意f'(1)=0,因此a+4b=0,得a=12 4分
(2)由(1)知f'(x)=48x3lnx(x>0),令f'(x)=0,解得x=1
当0<x<1时,f'(x)<0, f(x)单调递减;当x>1时,f'(x)>0, f(x)单调递增,
故 f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞) 8分
(3)由(2)知,f(x)在x=1处取得极小值f(1)=﹣3﹣c,此极小值也是最小值,
要使f(x)≥﹣2c2(x>0)恒成立,只需﹣3﹣c≥﹣2c2 10分
即2c2﹣c﹣3≥0,从而(2c﹣3)(c+1)≥0,解得![]() 或c≤﹣1
或c≤﹣1
所以c的取值范围为(﹣∞,﹣1]∪![]() 12分
12分


科目:高中数学 来源: 题型:
【题目】如图所示,已知椭圆C1:![]() +
+![]() =1,C2:
=1,C2:![]() +
+![]() =1(a>b>0)有相同的离心率,F(﹣
=1(a>b>0)有相同的离心率,F(﹣![]() , 0)为椭圆C2的左焦点,过点F的直线l与C1、C2依次交于A、C、D、B四点.
, 0)为椭圆C2的左焦点,过点F的直线l与C1、C2依次交于A、C、D、B四点.
(1)求椭圆C2的方程;
(2)求证:无论直线l的倾斜角如何变化恒有|AC|=|DB|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即![]() );如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
);如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
A. 4 B. 6 C. 8 D. 32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: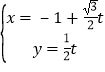 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判断f(x)的奇偶性并证明;
(II)若m=![]() ,判断f(x)在(3,+∞)的单调性(不用证明);
,判断f(x)在(3,+∞)的单调性(不用证明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)]?若存在,求出此时m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
(Ⅰ)求证:平面ABC1⊥平面A1C1CA;
(Ⅱ)设D是A1C1的中点,判断并证明在线段BB1上是否存在点E,使DE∥平面ABC1;若存在,求三棱锥E﹣ABC1的体积.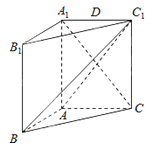
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是海面上一条南北方向的海防警戒线,在
是海面上一条南北方向的海防警戒线,在 ![]() 上点
上点 ![]() 处有一个水声监测点,另两个监测点
处有一个水声监测点,另两个监测点 ![]() 分别在
分别在 ![]() 的正东方向
的正东方向 ![]() 处和
处和 ![]() 处.某时刻,监测点
处.某时刻,监测点 ![]() 收到发自目标
收到发自目标 ![]() 的一个声波,
的一个声波,![]() 后监测点
后监测点 ![]() 后监测点
后监测点 ![]() 相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是
相继收到这一信号,在当时的气象条件下,声波在水中的传播速度是 ![]() .
.

(1)设 ![]() 到
到 ![]() 的距离为
的距离为 ![]() ,用
,用 ![]() 分别表示
分别表示 ![]() 到
到 ![]() 的距离,并求
的距离,并求 ![]() 的值;
的值;
(2)求目标 ![]() 的海防警戒线
的海防警戒线 ![]() 的距离(精确到
的距离(精确到 ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com