
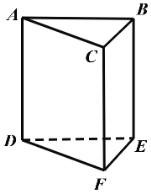
【题目】如图,一颗棋子从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,刚开始时,棋子在上底面点
,刚开始时,棋子在上底面点![]() 处,若移了
处,若移了![]() 次后,棋子落在上底面顶点的概率记为
次后,棋子落在上底面顶点的概率记为![]() .
.
(1)求![]() ,
,![]() 的值:
的值:
(2)求证:![]() .
.
【答案】(1)![]() ,
,![]() .(2)见解析
.(2)见解析
【解析】
(1)根据题意可知在上底面点![]() 处,移了
处,移了![]() 次可落在
次可落在![]() 的任意一点,可得
的任意一点,可得![]() ;分类讨论当第一次落在
;分类讨论当第一次落在![]() 或落在
或落在![]() 处的概率,即可得
处的概率,即可得![]() .
.
(2)根据移了![]() 次后棋子落在上底面顶点的概率为
次后棋子落在上底面顶点的概率为![]() ,可知落在下底面顶点的概率为
,可知落在下底面顶点的概率为![]() ,进而可得
,进而可得![]() 与
与![]() 的递推公式,利用构造数列法可得
的递推公式,利用构造数列法可得![]() 的通项公式;利用数学归纳法,即可证明
的通项公式;利用数学归纳法,即可证明![]() 成立.
成立.
(1)从三棱柱的一个项点沿棱移到相邻的另一个顶点的概率均为![]() ,棋子在上底面点
,棋子在上底面点![]() 处,移了
处,移了![]() 次可落在
次可落在![]() 的任意一点,
的任意一点,
所以![]() ,
,
若移![]() 次,则
次,则![]() 再移到上底面的概率为
再移到上底面的概率为![]() ,
,![]() 移到上底面的概率为
移到上底面的概率为![]() ,
,
所以![]() .
.
(2)证明:因为移了![]() 次后棋子落在上底面顶点的概率为
次后棋子落在上底面顶点的概率为![]() ,故落在下底面顶点的概率为
,故落在下底面顶点的概率为![]() .
.
于是移了![]() 次后棋子落在上底面顶点的概率为
次后棋子落在上底面顶点的概率为![]() .
.
从而![]() .
.
所以数列![]() 是等比数列,其首项为
是等比数列,其首项为![]() ,公比为
,公比为![]() .
.
所以![]() .
.
即![]() .用数学归纳法证明:
.用数学归纳法证明:
①当![]() 时,左式
时,左式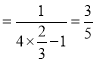 ,右式
,右式![]() ,因为
,因为![]() ,所以不等式成立.
,所以不等式成立.
当![]() 时,左式
时,左式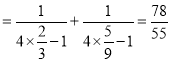 ,右式
,右式![]() ,因为
,因为![]() ,所以不等式成立.
,所以不等式成立.
②假设![]() 时,不等式成立,即
时,不等式成立,即![]() .
.
则![]() 时,左式
时,左式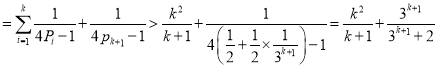 .
.
要证![]() ,只要证
,只要证![]() .
.
只要证![]() .
.
只要证![]() .
.
只要证![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() .即
.即![]() 时,不等式也成立.
时,不等式也成立.
由①②可知,不等式![]() 对任意的
对任意的![]() 都成立.
都成立.
不等式得证.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点F的直线L与C相交于A、B两点,当L的斜率为1时,坐标原点O到L的距离为
,过右焦点F的直线L与C相交于A、B两点,当L的斜率为1时,坐标原点O到L的距离为![]() .
.
(1)求椭圆的标准方程;
(2)在C上是否存在点P,使得当L绕F转到某一位置时,有![]() 成立?若存在,求出所有的P的坐标与L的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与L的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上贏得一片赞誉.我国某口罩生产厂商在加大生产的同时.狠抓质量管理,不定时抽查口罩质量,该厂质检人员从某日所生产的口罩中随机抽取了100个,将其质量指标值分成以下五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
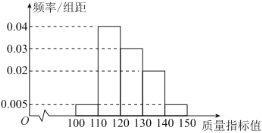
(1)规定:口罩的质量指标值越高,说明该口罩质量越好,其中质量指标值低于130的为二级口罩,质量指标值不低于130的为一级口罩.现从样本口罩中利用分层抽样的方法随机抽取8个口罩,再从中抽取3个,记其中一级口罩个数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在2020年“五一”劳动节前,甲,乙两人计划同时在该型号口罩的某网络购物平台上分别参加![]() 、
、![]() 两店各一个订单“秒杀”抢购,其中每个订单由
两店各一个订单“秒杀”抢购,其中每个订单由![]() 个该型号口罩构成.假定甲、乙两人在
个该型号口罩构成.假定甲、乙两人在![]() 、
、![]() 两店订单“秒杀”成功的概率分别为
两店订单“秒杀”成功的概率分别为![]() ,
, ,记甲、乙两人抢购成功的订单总数量、口罩总数量分别为
,记甲、乙两人抢购成功的订单总数量、口罩总数量分别为![]() ,
,![]() ,
,
①求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②求当![]() 的数学期望
的数学期望![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义域为
是定义域为![]() 的偶函数,对
的偶函数,对![]() ,有
,有![]() ,且当
,且当![]() 时,
时,![]() ,函数
,函数![]() .现给出以下命题:①
.现给出以下命题:①![]() 是周期函数;②
是周期函数;②![]() 的图象关于直线
的图象关于直线![]() 对称;③当
对称;③当![]() 时,
时,![]() 在
在![]() 内有一个零点;④当
内有一个零点;④当![]() 时,
时,![]() 在
在![]() 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com