
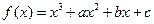 在
在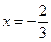 与
与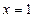 时都取得极值.
时都取得极值.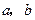 的值 (2)求函数
的值 (2)求函数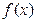 的单调区间;
的单调区间;  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 本小题共13分)
本小题共13分)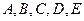 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.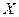 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加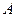 课程的人数,求
课程的人数,求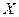 的分布列与数学期望.
的分布列与数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
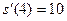 表示的意义是( )
表示的意义是( )| A.经过4s后物体向前走了10m | B.物体在前4s内的平均速度为10m/s |
| C.物体在第4s内向前走了10m | D.物体在第4s时的瞬时速度为10m/s |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
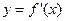 是函数
是函数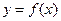 的导函数,且函数
的导函数,且函数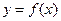 在点
在点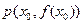 处的切线为:
处的切线为: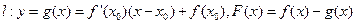 ,如果函数
,如果函数
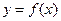 在区间
在区间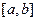 上的图像如图所示,且
上的图像如图所示,且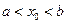 ,那么 ( )
,那么 ( )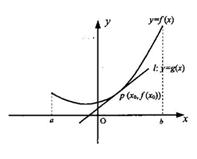
A.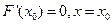 是 是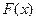 的极大值点 的极大值点 |
B.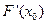 = =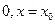 是 是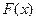 的极小值点 的极小值点 |
C.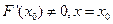 不是 不是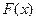 极值点 极值点 |
D.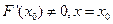 是 是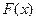 极值点 极值点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com