
【题目】等差数列{an}的前n项和Sn , 若a3+a7﹣a10=8,a11﹣a4=4,则S13等于( )
A.152
B.154
C.156
D.158
【答案】C
【解析】解:解法1:∵{an}为等差数列,设首项为a1 , 公差为d, ∴a3+a7﹣a10=a1+2d+a1+6d﹣a1﹣9d=a1﹣d=8①;a11﹣a4=a1+10d﹣a1﹣3d=7d=4②,
联立①②,解得a1= ![]() ,d=
,d= ![]() ;
;
∴s13=13a1+ ![]() d=156.
d=156.
解法2:∵a3+a7﹣a10=8①,a11﹣a4=4②,
①+②可得a3+a7﹣a10+a11﹣a4=12,
∵根据等差数列的性质a3+a11=a10+a4 ,
∴a7=12,
∴s13= ![]() ×13=13a7=13×12=156.
×13=13a7=13×12=156.
故选C.
【考点精析】本题主要考查了等差数列的前n项和公式的相关知识点,需要掌握前n项和公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点与
的一个焦点与![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一顶点为
为对角线的菱形的一顶点为![]() ,求
,求![]() 面积的最大值(
面积的最大值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式的大小关系正确的是( )
A.sin11°>sin168°
B.sin194°<cos160°
C.tan(﹣ ![]() )<tan(﹣
)<tan(﹣ ![]() )
)
D.cos(﹣ ![]() )>cos
)>cos ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
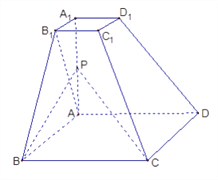
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的![]() 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温![]() (
(![]() )与该奶茶店的
)与该奶茶店的![]() 品牌饮料销量
品牌饮料销量![]() (杯),得到如表数据:
(杯),得到如表数据:
日期 | 1月11号 | 1月12号 | 1月13号 | 1月14号 | 1月15号 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程式
的线性回归方程式![]() ;
;
(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: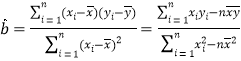 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱锥P﹣ABCD中,侧棱PA与底面ABCD所成的角的正切值为![]() .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.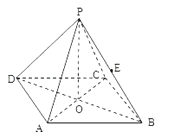
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com