
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,已知a= ![]() ,cosA=
,cosA= ![]() ,B=A+
,B=A+ ![]()
(1)求b的值;
(2)求△ABC的面积.
【答案】
(1)解:在△ABC中,∵0<A<π,cosA= ![]() ,B=A+
,B=A+ ![]() ,
,
∴sinA= ![]() =
= ![]() ,
,
sinB=sin(A+ ![]() )=cosA=
)=cosA= ![]() ,
,
又a= ![]() ,由
,由 ![]() 得,
得,
b= ![]() =
= ![]() =
= ![]() ;
;
(2)解:由(1)得,cosB=cos(A+ ![]() )=﹣sinA=﹣
)=﹣sinA=﹣ ![]() ,
,
∵A+B+C=π,∴C=π﹣(A+B),
∴sinC=sin(A+B)=sinAcosB+cosAsinB
= ![]() ×(﹣
×(﹣ ![]() )+
)+ ![]() ×
× ![]() =
= ![]() ,
,
∴△ABC的面积S= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由内角的范围、平方关系、诱导公式分别求出sinA、sinB的值,由正弦定理求出b的值;(2)由(1)和诱导公式求出cosB的值,由内角和定理、两角和的正弦公式求出sinC,代入三角形的面积公式求出△ABC的面积.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺丝,第一阶段,首先随意拧一个螺丝,接着拧它对角线上(距离它最远的,下同)螺丝,再随意拧第三个螺丝,第四个也拧它对角线上螺丝,第五个和第六个以此类推,但每个螺丝都不要拧死;第二阶段,将每个螺丝拧死,但不能连续拧相邻的2个螺丝。则不同的固定方式有 . 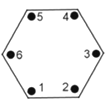
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 关于原点对称,
关于原点对称,![]() 恰为抛物线
恰为抛物线![]() :
:![]()
![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且线段
上,且线段![]() 的中点恰在
的中点恰在![]() 轴上,
轴上,![]() 的面积为8.若抛物线
的面积为8.若抛物线![]() 上存在点
上存在点![]() 使得
使得![]() ,则实数
,则实数![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ka﹣x(k,a为常数,a>0且a≠1)的图象过点A(0,1),B(3,8).
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() 是奇函数,求b的值;
是奇函数,求b的值;
(3)在(2)的条件下判断函数g(x)的单调性,并用定义证明你的结论;
(4)解不等式g(3x)+g(x﹣3﹣x2)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 和点P(4,2),直线l经过点P且与椭圆交于A,B两点.
和点P(4,2),直线l经过点P且与椭圆交于A,B两点.
(1)当直线l的斜率为 ![]() 时,求线段AB的长度;
时,求线段AB的长度;
(2)当P点恰好为线段AB的中点时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,其周长为
,其周长为![]() ,若点
,若点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)建立合适的平面直角坐标系,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若![]() 是射线
是射线![]() 上不同两点,
上不同两点, ![]() ,过点
,过点![]() 的直线与
的直线与![]() 交于
交于![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .证明:
.证明: ![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com