
分析 先利用余弦定理推导出a2=b2+3c2,再由正弦定理推导出$\frac{sin(A-B)}{sinC}$═$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$,由此能求出结果.
解答 解:∵在△ABC中,角A、B、C的对边分别为a、b、c,$\frac{a}{b}$+$\frac{2b}{a}$=3cosC,
∴$\frac{{a}^{2}+2{b}^{2}}{ab}=3×\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
整理,得a2=b2+3c2,
∴$\frac{sin(A-B)}{sinC}$=$\frac{sinAcosB-cosAsinb}{sinc}$
=$\frac{acosB-bcosA}{c}$=$\frac{a•\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}-b•\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}}{c}$
=$\frac{\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2c}-\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2c}}{c}$
=$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$=$\frac{{b}^{2}+3{c}^{2}-{b}^{2}}{{c}^{2}}$
=$\frac{3{c}^{2}}{{c}^{2}}$=3.
故答案为:3.
点评 本题考查三角形中两角差的正弦值与第三个角的正弦值的比值的求法,是中档题,解题时要认真审题,注意正弦定理和余弦定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
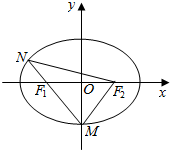 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2分别为椭圆的左、右焦点,M为椭圆的下顶点,直线MF1交椭圆与另一点N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2分别为椭圆的左、右焦点,M为椭圆的下顶点,直线MF1交椭圆与另一点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com