Question

已知数列{a_n}为正项等比数列，其前n项和为S_n，若S_n=1，S_3n=7，则a_n+1+a_n+2+a_n+3+…+a_4n=    ．

Answer 1

【答案】分析：由等比数列的性质可知，s_n，s_2n-s_n，s_3n-s_2n成等比数列结合S_n=1，S_3n=7，可求s_2n，同理可求s_4n-s_3n，进而可求s_4n，而a_n+1+a_n+2+a_n+3+…+a_4n=s_4n-s_n可求
解答：解：由等比数列的性质可知，s_n，s_2n-s_n，s_3n-s_2n成等比数列
∴
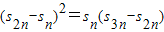
∵S_n=1，S_3n=7，
∴
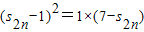
∴s_2n=3或s_2n=-2（舍去）
同理可求s_4n-s_3n=8
∴s_4n=15
则a_n+1+a_n+2+a_n+3+…+a_4n=s_4n-s_n=14
故答案为：14
点评：本题主要考查了等比 数列的性质的简单应用，利用该性质可以简化基本运算