
分析 (1)用辗转相除法直接求出两个数的最大公约数.
(2)利用秦九韶算法:f(x)=(((((2x+3)x+2)x+0)x-4)x+5,将x=2代入计算,即可得v4的值
解答 解:(1)用辗转相除法求2146与1813的最大公约数.
2146=1813×1+333 1813=333×5+148
333=148×2+37 148=37×4+0
所以2146与1813 的最大公约数是37-------------------------(5分)
(2)根据秦九韶算法,把多项式改写成如下形式:
f(x)=(((((2x+3)x+2)x+0)x-4)x+5
v0=2
v1=v0×2+3=7
v2=v0×2+2=16
v3=v1×2+0=32
v4=v2×2-4=60
所以当x=2时,v4=60.----------------(10分)
点评 本题考查辗转相除法求两个数的最大公约数,用秦九韶算法计算函数的函数值,基本知识的考查.


科目:高中数学 来源: 题型:选择题

| A. | 14 | B. | 07 | C. | 32 | D. | 43 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
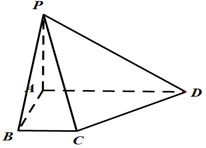 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$cm | B. | $\frac{{π}^{2}}{3}$cm | C. | $\frac{2π}{3}$cm | D. | $\frac{2{π}^{2}}{3}$cm |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com