
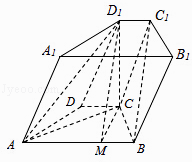
【题目】如图,在四棱锥ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C. 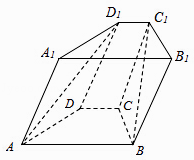
(1)求证:AD1⊥BC;
(2)若直线DD1与直线AB所成角为 ![]() ,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
【答案】
(1)证明:连接D1C,则D1C⊥平面ABCD,
∴D1C⊥BC
在等腰梯形ABCD中,连接AC
∵AB=2,BC=CD=1,AB∥CD
∴BC⊥AC
∴BC⊥平面AD1C
∴AD1⊥BC
(2)解法一:
∵AB∥CD∴ ![]()
∵CD=1∴ ![]()
在底面ABCD中作CM⊥AB,连接D1M,则D1M⊥AB,所以∠D1MC为平面ABC1D1与平面ABCD所成角的一个平面角
在Rt△D1CM中, ![]() ,
, ![]()
∴ ![]() ∴
∴ ![]()
即平面ABC1D1与平面ABCD所成角(锐角)的余弦函数值为 ![]()
解法二:
由(Ⅰ)知AC、BC、D1C两俩垂直,
∵AB∥CD∴ ![]() ∴
∴ ![]()
在等腰梯形ABCD中,连接AC因AB=2,BC=CD=1AB∥CD,
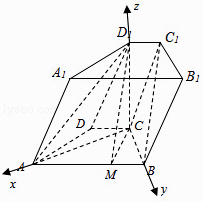
所以 ![]() ,建立如图空间直角坐标系,
,建立如图空间直角坐标系,
则 ![]() ,B(0,1,0),
,B(0,1,0), ![]()
设平面ABC1D1的一个法向量 ![]()
由 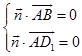 得
得 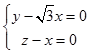
可得平面ABC1D1的一个法向量 ![]() .
.
又 ![]() 为平面ABCD的一个法向量.
为平面ABCD的一个法向量.
因此 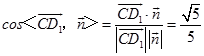
所以平面ABC1D1和平面ABCD所成的角(锐角)的余弦值为 ![]() .
.
【解析】(Ⅰ)证明:连接D1C,证明BC⊥平面AD1C,利用直线与平面垂直的性质定理证明AD1⊥BC.(Ⅱ)解法一:连接D1M,则D1M⊥AB,说明∠D1MC为平面ABC1D1与平面ABCD所成角的一个平面角,在Rt△D1CM中,求出 ![]() ,得到平面ABC1D1与平面ABCD所成角(锐角)的余弦函数值为
,得到平面ABC1D1与平面ABCD所成角(锐角)的余弦函数值为 ![]() .
.
解法二:
由(Ⅰ)知AC、BC、D1C两俩垂直,建立如图空间直角坐标系,求出相关点的坐标,求出平面ABC1D1的一个法向量,平面ABCD的法向量.通过向量的数量积求解平面ABC1D1和平面ABCD所成的角(锐角)的余弦值.
【考点精析】通过灵活运用直线与平面垂直的性质,掌握垂直于同一个平面的两条直线平行即可以解答此题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点. 
(1)求证:A1C∥平面BDC1;
(2)若AB⊥AC,且AB=AC= ![]() AA1 , 求二面角A﹣BD﹣C1的余弦值.
AA1 , 求二面角A﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=﹣2xln(1+
,g(x)=﹣2xln(1+ ![]() )﹣lnf(x).
)﹣lnf(x).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=0时,函数g(x)在定义域内是否存在零点?如果存在,求出该零点;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线C1:x=﹣2,圆C2:(x﹣1)2+(y﹣2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(Ⅰ)求C1 , C2的极坐标方程;
(Ⅱ)若直线C3的极坐标方程为θ= ![]() (ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.
(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=4x的焦点为F,过点F作直线l与抛物线分别交于两点A,B,若点M满足 ![]() =
= ![]() (
( ![]() +
+ ![]() ),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .
),过M作y轴的垂线与抛物线交于点P,若|PF|=2,则M点的横坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x﹣2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex﹣ ![]() ,a=f(﹣5),b=f(
,a=f(﹣5),b=f( ![]() ).c=f(
).c=f( ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a<b<c
B.c<a<b
C.c<a<b
D.b<a<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,
PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第4天和第5天共走了( )
A.60里
B.48里
C.36里
D.24里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2+ax+b|在区间[0,c]内的最大值为M(a,b∈R,c>0位常数)且存在实数a,b,使得M取最小值2,则a+b+c= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com