
【题目】已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N*,存在实数x使f(x)<2成立.
(1)求不等式f(x)>8的解;
(2)若α,β≥1,f(α)+f(β)=4,求证:![]() .
.
【答案】(1) {x|x![]() 或x
或x![]() };(2)证明见解析
};(2)证明见解析
【解析】
(1)由绝对值三角不等式可得|x﹣m|+|x|≥|m|,根据存在实数x使f(x)<2成立,求出实数m的值,然后解不等式f(x)>8即可.
(2)先由条件求出α+β=3,从而得到![]() ,再利用基本不等式求出最小值即可证明结论.
,再利用基本不等式求出最小值即可证明结论.
(1)因为|x﹣m|+|x|≥|(x﹣m)﹣x|=|m|,
所以由存在实数x使f(x)<2成立,可得|m|<2,
所以﹣2<m<2,因为m∈N*,所以m=1,
所以f(x)=|x﹣1|+|x|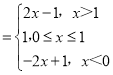 .
.
因为f(x)>8,所以![]() 或
或![]() ,
,
所以x![]() 或x
或x![]() ,
,
所以不等式的解集为{x|x![]() 或x
或x![]() };
};
(2)因为α,β≥1,所以f(α)+f(β)=2α﹣1+2β﹣1=4,则α+β=3,
所以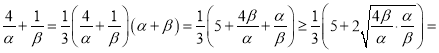 3,
3,
当且仅当![]() ,即α=2,β=1时取等号,
,即α=2,β=1时取等号,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0(m∈R).
(1)判断直线l与圆C的位置关系;
(2)设直线l与圆C交于A,B两点,若直线l的倾斜角为120°,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两县城![]() 和
和![]() 相距
相距![]() ,现计划在两县城外位于线段
,现计划在两县城外位于线段![]() 上选择一点
上选择一点![]() 建造一个两县城的公共垃圾处理厂,已知垃圾处理厂对城市的影响度与所选地点到城市的的距离关系最大,其他因素影响较小暂时不考虑,垃圾处理厂对城
建造一个两县城的公共垃圾处理厂,已知垃圾处理厂对城市的影响度与所选地点到城市的的距离关系最大,其他因素影响较小暂时不考虑,垃圾处理厂对城![]() 和城
和城![]() 的总影响度为对城
的总影响度为对城![]() 与城
与城![]() 的影响度之和. 记
的影响度之和. 记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理厂对城
处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理厂对城
,统计调查表明:垃圾处理厂对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数2.7;垃圾处理厂对城
的距离的平方成反比,比例系数2.7;垃圾处理厂对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ;且当垃圾处理厂
;且当垃圾处理厂![]() 与城
与城![]() 距离为
距离为![]() 时对城
时对城![]() 和城
和城![]() 的总影响度为0.029.
的总影响度为0.029.
(1) 将![]() 表示成
表示成![]() 的函数;
的函数;
(2) 讨论⑴中函数的单调性,并判断在线段![]() 上是否存在一点,使建在此处的垃圾处理厂对城
上是否存在一点,使建在此处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由.
的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 是两个不同的平面,
是两个不同的平面,![]() 、
、![]() 是两条不同的直线,有下列命题:
是两条不同的直线,有下列命题:
①如果![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;
;
②如果![]() ,
,![]() ,那么
,那么![]() ;
;
③如果![]() ,
,![]() ,那么
,那么![]() ;
;
④如果平面![]() 内有不共线的三点到平面
内有不共线的三点到平面![]() 的距离相等,那么
的距离相等,那么![]() ;
;
其中正确的命题是( )
A.①②B.②③C.②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,该动圆圆心
相切,该动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,抛物线在点A的切线与
两点,抛物线在点A的切线与![]() 交于点N,求
交于点N,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com