
【题目】已知函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称. (
对称. (![]() 为自然对数的底数)
为自然对数的底数)
(1)若![]() 的图象在点
的图象在点![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(2)若不等式![]() 恒成立,求正整数
恒成立,求正整数![]() 的最小值.
的最小值.
【答案】(1)e;(2)2.
【解析】
(1)根据反函数的性质,得出![]() ,再利用导数的几何意义,求出曲线
,再利用导数的几何意义,求出曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,构造函数
,构造函数![]() ,利用导数求出单调性,即可得出
,利用导数求出单调性,即可得出![]() 的值;
的值;
(2)设![]() ,求导
,求导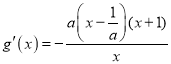 ,求出
,求出![]() 的单调性,从而得出最大值为
的单调性,从而得出最大值为![]() ,结合恒成立的性质,得出正整数
,结合恒成立的性质,得出正整数![]() 的最小值.
的最小值.
(1)根据题意,![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
所以函数![]() 的图象与
的图象与![]() 互为反函数,则
互为反函数,则![]() ,,
,,
设点![]() ,
,![]() ,又
,又![]() ,
,
当![]() 时,
时,![]() ,
,
曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,
,
即![]() ,代入点
,代入点![]() ,
,
得![]() ,即
,即![]() ,
,
构造函数![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
且![]() ,当
,当![]() 时,
时,![]() 单调递增,
单调递增,
而![]() , 故
, 故![]() 存在唯一的实数根
存在唯一的实数根![]() .
.
(2)由于不等式![]() 恒成立,
恒成立,
可设![]() ,
,
所以![]()
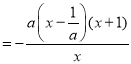 ,
,
令![]() ,得
,得![]() .
.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
因此函数![]() 在
在![]() 是增函数,在
是增函数,在![]()
![]() 是减函数.
是减函数.
故函数![]() 的最大值为
的最大值为![]()
![]() .
.
令![]() ,
,
因为![]() ,
,![]()
![]() ,
,
又因为![]() 在
在![]() 是减函数.
是减函数.
所以当![]() 时,
时,![]() .
.
所以正整数![]() 的最小值为2.
的最小值为2.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,则“1![]() 2”是“a2+a=3b2+2b”的( )
2”是“a2+a=3b2+2b”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,没售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
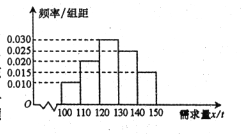
(Ⅰ)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(Ⅱ)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(Ⅲ)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如![]() ,则取
,则取![]() 的概率等于市场需求量落入
的概率等于市场需求量落入![]() 的频率),求
的频率),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,
,![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() ,
,![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() ,以
,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,如图所示,山区边界曲线为
,如图所示,山区边界曲线为![]() :
:![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
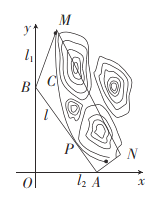
(1)设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,若公路
两点,若公路![]() 的斜率为-1,求
的斜率为-1,求![]() 的长;
的长;
(2)在(1)条件下,测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.直线
轴正半轴为极轴建立极坐标系.直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数a≠0,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)若![]() 且数列
且数列![]() 是单调递增数列,求实数a的取值范围;
是单调递增数列,求实数a的取值范围;
(3)若![]() 数列
数列![]() 满足:
满足: ![]() 对于任意给定的正整数k,是否存在p,
对于任意给定的正整数k,是否存在p,![]() ,使
,使![]() 若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com