
����Ŀ����ˮ��ֳ������ijˮ��Ʒ���¡���������ֳ�����IJ����Աȣ��ջ�ʱ�������ȡ��100 �����䣬��������ˮ��Ʒ�IJ�������λ��kg������Ƶ�ʷֲ�ֱ��ͼ���£�

��1����������ֳ��������������������A��ʾ�¼���������ֳ�������������50kg������ֳ���������������50kg��������A�ĸ��ʣ�
��2����д�������������������������ж��Ƿ���99%�İ�����Ϊ���������ֳ�����йأ�
�������50kg | �������50kg | |
����ֳ�� | ||
����ֳ�� |
��3�������������Ƶ�ʷֲ�ֱ��ͼ��������ֳ�����������λ���Ĺ���ֵ����ȷ��0.01����
���� ��
�� 
���𰸡���1��![]() ����2������������3��
����2������������3��![]() .
.
�������������������1������������¼����ʹ�ʽ��������¼�A�ĸ��ʹ���ֵ����2��д������������![]() �Ĺ۲�ֵ������ȷ����99%�İ�����Ϊ���������ֳ�����йأ���3�����Ƶ�ʷֲ�ֱ��ͼ������λ��Ϊ
�Ĺ۲�ֵ������ȷ����99%�İ�����Ϊ���������ֳ�����йأ���3�����Ƶ�ʷֲ�ֱ��ͼ������λ��Ϊ![]() ��
��
�����������1����B��ʾ�¼�������ֳ�������������![]() �� ��
�� �� ![]() ��ʾ�¼�������ֳ���������������
��ʾ�¼�������ֳ���������������![]() ��
��
������֪ ![]()
����ֳ�������������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ
![]()
��![]() �Ĺ���ֵΪ0.62
�Ĺ���ֵΪ0.62
����ֳ���������������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ
![]()
��![]() �Ĺ���ֵΪ0.66
�Ĺ���ֵΪ0.66
��ˣ��¼�A�ĸ��ʹ���ֵΪ![]()
��2�������������Ƶ�ʷֲ�ֱ��ͼ��������
����� | ����� | |
����ֳ�� | 62 | 38 |
����ֳ�� | 34 | 66 |
![]()
����![]()
����![]() �İ�����Ϊ���������ֳ�����йأ�
�İ�����Ϊ���������ֳ�����йأ�
��3����Ϊ����ֳ���������Ƶ�ʷֲ�ֱ��ͼ�У����������![]() ��ֱ��ͼ���Ϊ
��ֱ��ͼ���Ϊ
![]() ��
��
���������![]() ��ֱ��ͼ���Ϊ
��ֱ��ͼ���Ϊ
![]()
������ֳ�����������λ���Ĺ���ֵΪ
![]() ��
��
�㾦:��1�����ö����Լ��飬�ܹ��������Ƕ��ճ������е�ʵ�����������������ƶϺ�Ԥ�⣮�����Լ�����ǿ���������������Ƿ��й�ϵ�����ܽ�Ϊȷ�ظ��������жϵĿ��Ŷȣ���������Ĺ۲�ֵ![]() ֵԽ��˵�������������й�ϵ���Ŀ�����Խ��
ֵԽ��˵�������������й�ϵ���Ŀ�����Խ��
��2������Ƶ�ʷֲ�ֱ��ͼ����������λ����ƽ����ʱ��Ӧע�����㣺����ߵ�С�����εױ��е�ĺ����꼴����������λ����ߺ��ұߵ�С�����ε����������ȵģ���ƽ������Ƶ�ʷֲ�ֱ��ͼ�ġ����ġ�������Ƶ�ʷֲ�ֱ��ͼ��ÿ��С�����ε��������С�����εױ��е�ĺ�����֮�ͣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ���ڴ���m������n������m,n![]()
![]() ,n
,n![]() 2��,��Щ�����ɫ��ȫ����ͬ���ֽ��ڴ��е�����������ȡ������������ͼ��ʾ�ı��Ϊ1,2,3��������m+n�ij����ڣ����е�k��ȡ�������Ϊk�ij��루k=1,2,3��������m+n��.
2��,��Щ�����ɫ��ȫ����ͬ���ֽ��ڴ��е�����������ȡ������������ͼ��ʾ�ı��Ϊ1,2,3��������m+n�ij����ڣ����е�k��ȡ�������Ϊk�ij��루k=1,2,3��������m+n��.
![]()
��1��������Ϊ2�ij����ڷŵ��Ǻ���ĸ���p;
��2���������x��ʾ���һ��ȡ���ĺ������ڳ����ŵĵ�����E(x)��x����ѧ������֤�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�tanA���ԩ�4Ϊ�����4Ϊ������ĵȲ����еĹ��tanB���� ![]() Ϊ�����9Ϊ������ĵȱ����й��ȣ�������������ǣ� ��
Ϊ�����9Ϊ������ĵȱ����й��ȣ�������������ǣ� ��
A.�۽�������
B.���������
C.����ֱ��������
D.���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ��һ��������n����Pn��n��Sn�����ں���f��x��=x2+2x��ͼ���ϣ���an��an+1�ĵȲ�����Ϊkn ��
��1��������{an}��ͨ�ʽ��
��2���� ![]() ��������{bn}��ǰn���Tn��
��������{bn}��ǰn���Tn��
��3���輯�� ![]() ���Ȳ�����{cn}������һ��cn��A��B������c1��A��B�е���С������110��c10��115����{cn}��ͨ�ʽ��
���Ȳ�����{cn}������һ��cn��A��B������c1��A��B�е���С������110��c10��115����{cn}��ͨ�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=x2��2x��4lnx����f��x���ĵ�����������Ϊ�� ��
A.����1��0��
B.����1��0���ȣ�2��+�ޣ�
C.��2��+�ޣ�
D.��0��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
������![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��������![]() �ĵ������䣻
�ĵ������䣻
�����躯��![]() ������������
������������![]() ������
������![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ���ˮ����lʱ��������ˮ��4�ף�ˮ���8�ף�ˮλ����1��ˮ���Ϊ�� �� 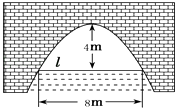
A.![]() ��
��
B.2 ![]() ��
��
C.3 ![]() ��
��
D.4 ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
��
��1����![]() ��������
��������![]() ��
��![]() �������߷��̣�
�������߷��̣�
��2������![]() ʱ��
ʱ�� ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ������ϵxOy�У�Բ����C�IJ�������Ϊ ![]() ����Ϊ��������ֱ��l��������P��2��3������б��Ϊ
����Ϊ��������ֱ��l��������P��2��3������б��Ϊ ![]() ��
��
��1��д��ֱ��l�IJ������̺�Բ�ı����̣�
��2����ֱ��l��Բ�ཻ��A��B���㣬���PA������PB����ֵ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com